
分析 (1)利用三角恒等变换公式化简已知等式,算出sinB=$\frac{\sqrt{3}}{2}$,结合B是△ABC的内角可B=$\frac{π}{3}$或B=$\frac{2π}{3}$;
(2)根据正弦定理的面积公式,算出边c=5.再利用余弦定理b2=a2+c2-2accosB的式子,代入数据即可算出边b的值.
解答 解:(1)由4sinB•sin2($\frac{π}{4}$+$\frac{B}{2}$)+cos2B=1+$\sqrt{3}$,
得2sinB•[1-cos($\frac{π}{2}$+B)]+1-2sin2B=1+$\sqrt{3}$,可得sinB=$\frac{\sqrt{3}}{2}$,
又∵B是△ABC的内角,∴B=$\frac{π}{3}$或B=$\frac{2π}{3}$;
(2)∵a=8,S=10$\sqrt{3}$,
∴$\frac{1}{2}$acsinB=$\frac{1}{2}$×8×c×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$,解之得c=5
∵由余弦定理,得b2=a2+c2-2accosB
∴当B=$\frac{π}{3}$时,b=$\sqrt{64+25-2×8×5×\frac{1}{2}}$=7;
当B=$\frac{2π}{3}$时,b=$\sqrt{64+25-2×8×5×cos\frac{2π}{3}}$=$\sqrt{129}$.
即边b的值等于7或$\sqrt{129}$.
点评 本题给出三角形中角B的三角等式,求角B的大小,并在已知面积的情况下求边b.着重考查了三角恒等变换、正余弦定理解三角形和三角形的面积公式等知识,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 3 | D. | 0或3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1008>b1008 | B. | a1008≥b1008 | ||
| C. | a1008<b1008 | D. | 以上答案均有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{f(m)}{m}<\frac{f(n)}{n}$ | B. | $\frac{f(m)}{m}>\frac{f(n)}{n}$ | C. | $\frac{f(m)}{n}>\frac{3f(n)}{m}$ | D. | $\frac{f(m)}{n}<\frac{f(n)}{m}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
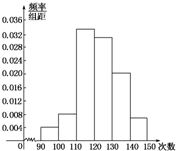 为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 1023 | D. | -1023 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ABCD是矩形 | B. | ABCD是菱形 | ||
| C. | ABCD是正方形 | D. | ABCD是平行四边形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com