
分析 (1)由条件利用两角和的正切公式求得tanα 的值,再根据sin2α+cos2α=1,0$<α<\frac{π}{2}$<β<π,求得cosα的值.
(2)由条件同角三角函数的基本关系求得cos(α+β),再利用两角差的正弦公式求得sinβ=sin[(α+β)-α]的值.
解答 解:(1)把tan$\frac{α}{2}$=$\frac{1}{2}$代入tanα=$\frac{2tan\frac{α}{2}}{1{-tan}^{2}\frac{α}{2}}$,求得tanα=$\frac{4}{3}$=$\frac{sinα}{cosα}$,再根据sin2α+cos2α=1,0$<α<\frac{π}{2}$<β<π,
求得sinα=$\frac{4}{5}$,cosα=$\frac{3}{5}$.
(2)由0$<α<\frac{π}{2}$<β<π,可得$\frac{π}{2}$<α+β<$\frac{3π}{2}$,再根据sin(α+β)=$\frac{5}{13}$,
可得α+β∈($\frac{π}{2}$,π),∴cos(α+β)=-$\frac{12}{13}$,
∴sinβ=sin[(α+β)-α]=sin(α+β)cosα-cos(α+β)sinα=$\frac{5}{13}×\frac{3}{5}$-(-$\frac{12}{13}$)×$\frac{4}{5}$=$\frac{63}{65}$.
点评 本题主要考查同角三角函数的基本关系,两角差的三角公式的应用,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{27}{4}$ | B. | $\frac{9}{4}$ | C. | $\frac{27\sqrt{3}}{4}$ | D. | $\frac{9\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
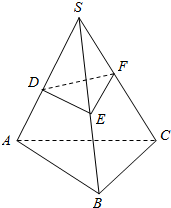 如图.D、E、F分别是三棱锥S-ABC,侧棱SA、SB、SC上的点.且SD:DA=SE:EB=CF:FS=2:1.那么过D、E、F的 平面截三棱锥S-ABC所得上下两部分体积的比为4:23.
如图.D、E、F分别是三棱锥S-ABC,侧棱SA、SB、SC上的点.且SD:DA=SE:EB=CF:FS=2:1.那么过D、E、F的 平面截三棱锥S-ABC所得上下两部分体积的比为4:23.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y=0 | B. | $x-2y-\frac{5}{2}=0$ | C. | 2x-y-2=0 | D. | $x-4y-\frac{9}{2}=0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
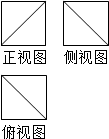 将某正方体工件进行切削,把它加工成一个体积尽可能大的新工件,新工件的三视图如图所示,则原工件材料的利用率为〔材料的利用率=$\frac{新工件的体积}{原工件的体积}$〕( )
将某正方体工件进行切削,把它加工成一个体积尽可能大的新工件,新工件的三视图如图所示,则原工件材料的利用率为〔材料的利用率=$\frac{新工件的体积}{原工件的体积}$〕( )| A. | $\frac{7}{8}$ | B. | $\frac{6}{7}$ | C. | $\frac{5}{6}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com