
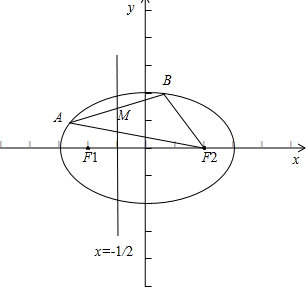
 如图,F1,F2是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左、右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线l:x=-$\frac{1}{2}$上.
如图,F1,F2是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左、右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线l:x=-$\frac{1}{2}$上.分析 (1)先求得A点的横坐标为-1,代入椭圆方程$\frac{{x}^{2}}{2}$+y2=1,解得y的值,可得A的纵坐标,再根据中点公式求得M的坐标.
(2)当AB垂直于x轴时,易得$\overrightarrow{{F}_{2}A}$•$\overrightarrow{{F}_{2}B}$的值.当AB不垂直于x轴时,设AB的斜率为k,M(-$\frac{1}{2}$,m),由$\left\{\begin{array}{l}{\frac{{{x}_{1}}^{2}}{2}{{+y}_{1}}^{2}=1}\\{\frac{{{x}_{2}}^{2}}{2}{{+y}_{2}}^{2}=1}\end{array}\right.$可得 k=$\frac{1}{4m}$,可得AB的方程为y=$\frac{1}{4m}$x+$\frac{{8m}^{2}+1}{8m}$ ①.把①代入椭圆方程化简利用韦达定理,由判别式大于零,求得m2的范围,化简 $\overrightarrow{{F}_{2}A}$•$\overrightarrow{{F}_{2}B}$ 为 $\frac{3{(8m}^{2}+1)+8}{8(1{+8m}^{2})}$.令t=1+8m2,则1<t<8,再根据函数的单调性求得 $\overrightarrow{{F}_{2}A}$•$\overrightarrow{{F}_{2}B}$=$\frac{1}{8}$[3t+$\frac{8}{t}$]的范围.
解答 解:(1)∵B的坐标为(0,1),且线段AB的中点M在直线l:x=-$\frac{1}{2}$上,
∴A点的横坐标为-1,
代入椭圆方程$\frac{{x}^{2}}{2}$+y2=1,解得y=±$\frac{\sqrt{2}}{2}$,故点A(-1,$\frac{\sqrt{2}}{2}$)或点A(-1,-$\frac{\sqrt{2}}{2}$).
∴线段AB的中点M(-$\frac{1}{2}$,$\frac{1}{2}$+$\frac{\sqrt{2}}{4}$)或(-$\frac{1}{2}$,$\frac{1}{2}$-$\frac{\sqrt{2}}{4}$).
(2)由于F1(-1,0),F2(1,0),当AB垂直于x轴时,AB的方程为x=-$\frac{1}{2}$,点A(-$\frac{1}{2}$,-$\sqrt{\frac{7}{8}}$)、
B(-$\frac{1}{2}$,$\sqrt{\frac{7}{8}}$),
求得$\overrightarrow{{F}_{2}A}$•$\overrightarrow{{F}_{2}B}$=$\frac{11}{8}$.
当AB不垂直于x轴时,设AB的斜率为k,M(-$\frac{1}{2}$,m),A(x1,y1 ),B (x2,y2),
由$\left\{\begin{array}{l}{\frac{{{x}_{1}}^{2}}{2}{{+y}_{1}}^{2}=1}\\{\frac{{{x}_{2}}^{2}}{2}{{+y}_{2}}^{2}=1}\end{array}\right.$可得 (x1+x2)+2(y1+y2)•$\frac{{y}_{1}{-y}_{2}}{{x}_{1}{-x}_{2}}$=0,∴-1=-4mk,即 k=$\frac{1}{4m}$,
故AB的方程为 y-m=$\frac{1}{4m}$(x+$\frac{1}{2}$),即 y=$\frac{1}{4m}$x+$\frac{{8m}^{2}+1}{8m}$ ①.
再把①代入椭圆方程$\frac{{x}^{2}}{2}$+y2=1,可得x2+x+$\frac{1}{4}$•$\frac{{({8m}^{2}+1)}^{2}-6{4m}^{2}}{{8m}^{2}+1}$=0.
由判别式△=1-$\frac{{({8m}^{2}+1)}^{2}-6{4m}^{2}}{{8m}^{2}+1}$>0,可得0<m2<$\frac{7}{8}$.
∴x1+x2=-1,x1•x2=$\frac{{({8m}^{2}+1)}^{2}-6{4m}^{2}}{{8m}^{2}+1}$,y1•y2=($\frac{1}{4m}$•x1+$\frac{{8m}^{2}+1}{8m}$ )($\frac{1}{4m}$x2+$\frac{{8m}^{2}+1}{8m}$ ),
∴$\overrightarrow{{F}_{2}A}$•$\overrightarrow{{F}_{2}B}$=(x1-1,y1 )•(x2-1,y2)=x1•x2+y1•y2-(x1+x2)+1=$\frac{3{(8m}^{2}+1)+8}{8(1{+8m}^{2})}$.
令t=1+8m2,则1<t<8,∴$\overrightarrow{{F}_{2}A}$•$\overrightarrow{{F}_{2}B}$=$\frac{{3t}^{2}+8}{8t}$=$\frac{1}{8}$[3t+$\frac{8}{t}$].
再根据$\frac{1}{8}$[3t+$\frac{8}{t}$]在(1,$\sqrt{\frac{8}{3}}$)上单调递减,在($\sqrt{\frac{8}{3}}$,8)上单调递增求得$\frac{1}{8}$[3t+$\frac{8}{t}$]的范围为[$\frac{\sqrt{6}}{2}$,$\frac{25}{8}$).
综上可得,$\frac{1}{8}$[3t+$\frac{8}{t}$]的范围为[$\frac{\sqrt{6}}{2}$,$\frac{25}{8}$).
点评 本题主要考查本题主要考查椭圆的定义、标准方程,以及简单性质的应用,两个向量的数量积公式的应用,直线和二次曲线的关系,考查计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥A-DCBE中,AC⊥BC,底面DCBE为平行四边形,DC⊥平面ABC.
如图,在四棱锥A-DCBE中,AC⊥BC,底面DCBE为平行四边形,DC⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在底面为菱形ABCD的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AB=2,A1B=A1D=2$\sqrt{2}$.
如图,在底面为菱形ABCD的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AB=2,A1B=A1D=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{3}{2}$] | B. | (1,$\frac{3}{2}$] | C. | (1,$\frac{3}{4}$] | D. | (1,$\frac{7}{4}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com