
分析 (1)将k=-1代入,求出函数f(x)的表达式,得到函数的导数,求出斜率f′(1)=2,代入点斜式方程,从而求出切线的方程;
(2)先求出函数的导数,通过讨论x的范围,从而求出函数的单调区间和最值.
解答 解:(1)k=-1时,f(x)=x-$\frac{1}{x}$,
∴f′(x)=1+$\frac{1}{{x}^{2}}$,f′(1)=2,
∴切线方程为:y=2(x-1);
(2)k>0时,f′(x)=1-$\frac{k}{{x}^{2}}$=$\frac{{x}^{2}-k}{{x}^{2}}$,
x>0时:令f′(x)>0,解得:x>$\sqrt{k}$,令f′(x)<0,解得:0<x<$\sqrt{k}$,
∴f(x)在(0,$\sqrt{k}$)递减,在($\sqrt{k}$+∞)递增,
x<0时:令f′(x)>0,解得:x<-$\sqrt{k}$,令f′(x)<0,解得:0<x<$\sqrt{k}$,
∴f(x)在(-∞,-$\sqrt{k}$)递增,在(-$\sqrt{k}$,0)递减;
当x<0时:f(x)极大值=f(-$\sqrt{k}$)=-2$\sqrt{k}$,
当x>0时:f(x)极小值=f($\sqrt{k}$)=2$\sqrt{k}$.
点评 本题考查了利用导数求曲线的切线问题,考查利用导数研究函数的单调性,极值问题,考查分类讨论思想,是一道中档题.


科目:高中数学 来源: 题型:解答题
 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=AlC1=l,AAl=4,BBl=2,CCl=3.
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=AlC1=l,AAl=4,BBl=2,CCl=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
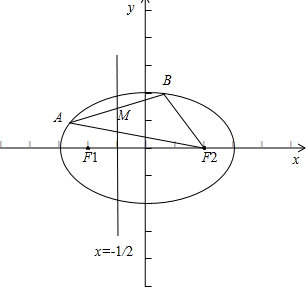 如图,F1,F2是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左、右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线l:x=-$\frac{1}{2}$上.
如图,F1,F2是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左、右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线l:x=-$\frac{1}{2}$上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方体ABCD-A1B1C1D1中,E,F分别是AB,BC的中点.求证:
如图,正方体ABCD-A1B1C1D1中,E,F分别是AB,BC的中点.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com