
设函数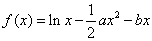
(1)当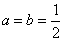 时,求函数
时,求函数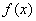 的单调区间;
的单调区间;
(2)令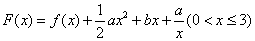 ,其图象上任意一点P(x0,y0)处切线的斜率k≤
,其图象上任意一点P(x0,y0)处切线的斜率k≤ 恒成立,求实数
恒成立,求实数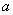 的取值范围;
的取值范围;
(3)当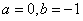 时,方程
时,方程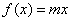 在区间内有唯一实数解,求实数
在区间内有唯一实数解,求实数 的取值范围.
的取值范围.
证明:(1)f(1)-2f(2)+f(3)=1+p+q-2(4+2p+q)+9+3p+q=2.
解:(1)依题意知,f(x)的定义域为(0,+∞).
当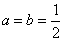 时,f(x)=lnx-
时,f(x)=lnx-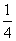 x2-
x2- x,f′(x)=
x,f′(x)=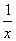 -
- x-
x- =
=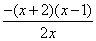 ,
,
令f′(x)=0,解得x=1或x=-2(舍去).…………2分
当0<x<1时,f′(x)>0,当x>1时,f′(x)<0,
所以f(x)的单调递增区间为(0,1),单调递减区间为(1,+∞).
(2)F(x)=lnx+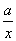 ,x∈(0,3],
,x∈(0,3],
则有k=F′(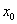 )=
)=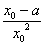 ≤
≤ 在(0,3]上恒成立.
在(0,3]上恒成立.
所以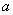
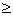
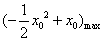 ,
,
当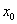 =1时,-
=1时,- x
x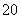 +
+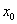 取得最大值
取得最大值 .
. 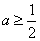 .
.
(3)当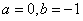 时,f(x)=lnx+x,
时,f(x)=lnx+x,
由f(x)=mx,得lnx+x=mx,
又x>0,∴m=1+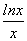 .
.
要使方程f(x)=mx在区间上有唯一实数解.
只需m=1+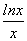 有唯一实数解,令g(x)=1+
有唯一实数解,令g(x)=1+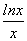 (x>0),∴g′(x)=
(x>0),∴g′(x)=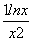 ,
,
由g′(x)>0,得0<x<e.g′(x)<0,得x>e,
∴g(x)在区间上是增函数,在区间上是减函数.
g(1)=1,g(e2)=1+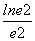 =1+
=1+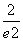 ,g(e)=1+
,g(e)=1+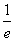 ,
,
∴m=1+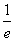 或1≤m<1+
或1≤m<1+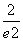 .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
某地区有小学21所,中学14所,大学7所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(1)求应从小学、中学、大学中分别抽取的学校数目;
(2)若从抽取的6所学校中随机抽取2所学校做进一步数据分析.
(ⅰ)列出所有可能的抽取结果;
(ⅱ)求抽取的2所学校均为小学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知f(x)=x2+px+q.
(1)求证:f(1)-2f(2)+f(3)=2;
(2)求证:|f(1)|、|f(2)|、|f(3)|中至少有一个不小于 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com