
已知f(x)=x2+px+q.
(1)求证:f(1)-2f(2)+f(3)=2;
(2)求证:|f(1)|、|f(2)|、|f(3)|中至少有一个不小于 .
.
科目:高中数学 来源: 题型:
已知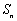 是等比数列
是等比数列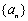 的前
的前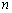 项和,
项和, ,
,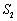 ,
, 成等差数列,且
成等差数列,且 .
.
(Ⅰ)求数列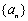 的通项公式;
的通项公式;
(Ⅱ)是否存在正整数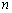 ,使得
,使得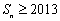 ?若存在,求出符合条件的所有
?若存在,求出符合条件的所有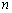 的集合;若不存在,说明理由.
的集合;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数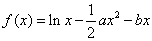
(1)当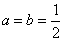 时,求函数
时,求函数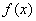 的单调区间;
的单调区间;
(2)令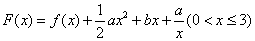 ,其图象上任意一点P(x0,y0)处切线的斜率k≤
,其图象上任意一点P(x0,y0)处切线的斜率k≤ 恒成立,求实数
恒成立,求实数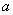 的取值范围;
的取值范围;
(3)当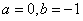 时,方程
时,方程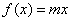 在区间内有唯一实数解,求实数
在区间内有唯一实数解,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
某旅行社在暑假期间推出如下旅游团组团办法:达到100人的团体,每人收费1000元。如果团体的人数超过100人,那么每超过1人,每人平均收费降低5元,但团体人数不能超过180人,如何组团可使旅行社的收费最多? (不到100人不组团)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com