
| nr+1-(n-1)r+1 |
| r+1 |
| (n+1)r+1-nr+1 |
| r+1 |
| 3 |
| 2 |
| 3 | 81 |
| 3 | 82 |
| 3 | 83 |
| 3 | 125 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 1 |
| n |
| 1 |
| n |
| r+1 |
| n |
| (n+1)r+1-nr+1 |
| r+1 |
| 1 |
| n |
| nr+1-(n-1)r+1 |
| r+1 |
| nr+1-(n-1)r+1 |
| r+1 |
| (n+1)r+1-nr+1 |
| r+1 |
| 1 |
| 3 |
| 3 |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3 | 81 |
| 3 |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3 | 82 |
| 3 |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3 | 83 |
| 3 |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3 | 125 |
| 3 |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |


 «Š«…∂ŠĻŕ÷‹≤‚‘¬Ņľ÷ĪÕ®÷–ŅľŌĶŃ–īūįł
«Š«…∂ŠĻŕ÷‹≤‚‘¬Ņľ÷ĪÕ®÷–ŅľŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
| nr+1-(n-1)r+1 |
| r+1 |
| (n+1)r+1-nr+1 |
| r+1 |
| 3 |
| 2 |
| 3 | 81 |
| 3 | 82 |
| 3 | 83 |
| 3 | 125 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ2013ńÍ∆’Õ®łŖĶ»—ß–£’–…ķ»ęĻķÕ≥“ĽŅľ ‘ļĢĪĪĺŪņŪ ż Ő‚–Õ£ļ044
…Ťn «’ż’Ż ż£¨rő™’ż”–ņŪ ż£ģ
(ĘŮ)«ůļĮ żf(x)£Ĺ(1£ęx)r+1£≠(r£ę1)x£≠1(x£ĺ£≠1)Ķń◊Ó–°÷Ķ£Ľ
(ĘÚ)÷§√ų£ļ![]() £Ľ
£Ľ
(Ęů)…Ťx° R£¨ľ«[x]ő™≤Ľ–°”ŕxĶń◊Ó–°’Ż ż£¨ņż»Á[2]£Ĺ2£¨[¶–]£Ĺ4£¨[£≠![]() ]£Ĺ£≠1£ģŃÓS£Ĺ
]£Ĺ£≠1£ģŃÓS£Ĺ![]() £ę
£ę![]() £ę
£ę![]() £ę°≠£ę
£ę°≠£ę![]() £¨«ů[S]Ķń÷Ķ£ģ
£¨«ů[S]Ķń÷Ķ£ģ
(≤őŅľ żĺ›£ļ![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() )
)
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļĹ‚īūŐ‚
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ2013ńÍļĢĪĪ °łŖŅľ ż—ß ‘ĺŪ£®ņŪŅ∆£©£®Ĺ‚őŲįś£© Ő‚–Õ£ļĹ‚īūŐ‚
 £Ľ
£Ľ £ģŃÓ
£ģŃÓ Ķń÷Ķ£ģ
Ķń÷Ķ£ģ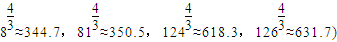 £ģ
£ģ≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com