
 ;
; .令
.令 的值.
的值.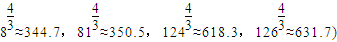 .
.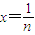 代入并化简得
代入并化简得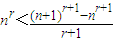 ,再令
,再令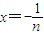 得,
得,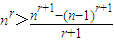 ,即结论得到证明;
,即结论得到证明;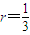 ,n分别取值81,82,83,…,125,分别列出不等式,再将各式相加得,
,n分别取值81,82,83,…,125,分别列出不等式,再将各式相加得,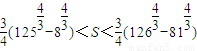 ,再由参考数据和条件进行求解.
,再由参考数据和条件进行求解.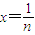 (这时x>-1且x≠0),得
(这时x>-1且x≠0),得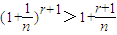 .
.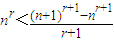 ,②
,②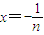 (这时x>-1且x≠0),
(这时x>-1且x≠0),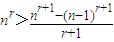 ,③
,③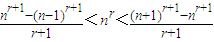 ,④
,④ ,n分别取值81,82,83,…,125,
,n分别取值81,82,83,…,125,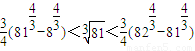 ,
,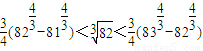 ,
,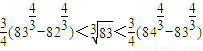 ,…
,…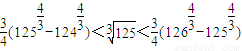 ,
,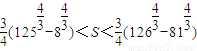 .
.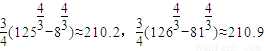


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
| nr+1-(n-1)r+1 |
| r+1 |
| (n+1)r+1-nr+1 |
| r+1 |
| 3 |
| 2 |
| 3 | 81 |
| 3 | 82 |
| 3 | 83 |
| 3 | 125 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2013年普通高等学校招生全国统一考试湖北卷理数 题型:044
设n是正整数,r为正有理数.
(Ⅰ)求函数f(x)=(1+x)r+1-(r+1)x-1(x>-1)的最小值;
(Ⅱ)证明:![]() ;
;
(Ⅲ)设x∈R,记[x]为不小于x的最小整数,例如[2]=2,[π]=4,[-![]() ]=-1.令S=
]=-1.令S=![]() +
+![]() +
+![]() +…+
+…+![]() ,求[S]的值.
,求[S]的值.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:湖北 题型:解答题
| nr+1-(n-1)r+1 |
| r+1 |
| (n+1)r+1-nr+1 |
| r+1 |
| 3 |
| 2 |
| 3 | 81 |
| 3 | 82 |
| 3 | 83 |
| 3 | 125 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com