
设n是正整数,r为正有理数.
(Ⅰ)求函数f(x)=(1+x)r+1-(r+1)x-1(x>-1)的最小值;
(Ⅱ)证明:![]() ;
;
(Ⅲ)设x∈R,记[x]为不小于x的最小整数,例如[2]=2,[π]=4,[-![]() ]=-1.令S=
]=-1.令S=![]() +
+![]() +
+![]() +…+
+…+![]() ,求[S]的值.
,求[S]的值.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
| nr+1-(n-1)r+1 |
| r+1 |
| (n+1)r+1-nr+1 |
| r+1 |
| 3 |
| 2 |
| 3 | 81 |
| 3 | 82 |
| 3 | 83 |
| 3 | 125 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:湖北 题型:解答题
| nr+1-(n-1)r+1 |
| r+1 |
| (n+1)r+1-nr+1 |
| r+1 |
| 3 |
| 2 |
| 3 | 81 |
| 3 | 82 |
| 3 | 83 |
| 3 | 125 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2013年湖北省高考数学试卷(理科)(解析版) 题型:解答题
 ;
; .令
.令 的值.
的值.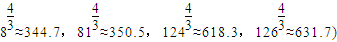 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com