
分析 (1)由已知可得函数图象关于直线x=1对称,开口朝上,最小值为1,进而构造关于a,b的方程,解得a,b的值;
(2)若g(x)=f(x)-mx在[2,4]上为单调函数,则$\frac{m+2}{2}$≤2,或$\frac{m+2}{2}$≥4,解各实数m的取值范围.
解答 解:(1)∵函数f(x)满足对任意的实数x都有f(1-x)=f(1+x),
故函数图象关于直线x=1对称,
即$\frac{2}{2{a}^{2}}$=1,
又∵f(x)的值域为[1,+∞),
故a>0且$\frac{4a(2+b)-\frac{4}{{a}^{2}}}{4a}$=1,
解得:a=1,b=0;
(2)由(1)得f(x)=x2-2x+2,
∴g(x)=f(x)-mx=x2-(m+2)x+2,
函数图象关于直线x=$\frac{m+2}{2}$对称,
若g(x)在[2,4]上为单调函数,
则$\frac{m+2}{2}$≤2,或$\frac{m+2}{2}$≥4,
解得:m∈(-∞,2]∪[6,+∞)
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:解答题
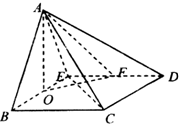 在四棱锥A-BCDE中,底面BCDE为菱形,侧面ABE为等边三角形,且侧面ABE⊥底面BCDE,O,F分别为BE,DE的中点.
在四棱锥A-BCDE中,底面BCDE为菱形,侧面ABE为等边三角形,且侧面ABE⊥底面BCDE,O,F分别为BE,DE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{27}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com