
分析 (1)利用二项展开式的通项公式求出展开式的通项,求出展开式中第3项与第5项的系数列出方程求出n的值.
(2)利用两边夹定理,设出第r+1项为系数的绝对值最大的项,即可列出关于r的不等式,解得即可,
(3)利用二项式定理求得结果.
解答 解:(1)($\sqrt{{x}^{3}}$-$\frac{2}{x}$)n的展开式中通项公式为Tr+1=Cnr${x}^{\frac{3n-5r}{2}}$(-2)r,
∴展开式中第3项与第5项的系数分别为22Cn2,24Cn4,
∴24Cn4:22Cn2=14:1,
即2Cn4=7Cn2,
解得n=9,
∴展开式中通项公式为Tr+1=C9r${x}^{\frac{27-5r}{2}}$(-2)r,
令$\frac{27-5r}{2}$=6,
解得r=3,
∴展开式中x6的系数为C93(-2)3=-224,
(2)设第r项的系数的绝对值最大,
则C9r-12r-1≤C9r2r≤C9r+12r+1,
解得r=9,
则展开式中系数绝对值最大的项第10项,
(3)9+9C92+81C93+…+98C99=$\frac{1}{9}$(9C91+92C92+93C93+…+99C99)
=$\frac{1}{9}$(90C90+9C91+92C92+93C93+…+99C99)=$\frac{1}{9}$[(1+9)9-1]=$\frac{1{0}^{9}-1}{9}$.
点评 本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:解答题
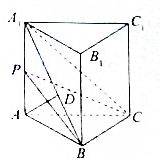 如图,在直三棱柱ABC-A1B1C1中,AB=BC=2,AA1=2$\sqrt{3}$,CB⊥AB,D为线段A1B上一点,且A1D=3,P为AA1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=2,AA1=2$\sqrt{3}$,CB⊥AB,D为线段A1B上一点,且A1D=3,P为AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AA1⊥底面ABCD,AB=2,AA1=BC=4,∠ABC=60°,点E为BC中点,点F为B1C1中点.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AA1⊥底面ABCD,AB=2,AA1=BC=4,∠ABC=60°,点E为BC中点,点F为B1C1中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
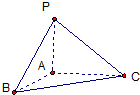 如图,三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,PA=AB,则直线PB与平面ABC所成的角是( )
如图,三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,PA=AB,则直线PB与平面ABC所成的角是( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com