Question

7．若定义在[0，+∞）上的函数f（x）满足：当0≤x＜2时，f（x）=$\sqrt{1-{{（x-1）}^2}}$，当2^k-2≤x＜2^k+1-2（k∈N^*）时，f（x）=2f（$\frac{x-2}{2}$），则函数F（x）=|${\frac{lnx}{x}}$|-f（x）在区间（0，2016）的零点个数为19．

Answer 1

分析 推导出（x-（2^k-1+2^k-1））²+y²=4^k-1（y≥0），令$g（x）=\frac{lnx}{x}$，$g'（x）=\frac{1-lnx}{x^2}$，作出$y=|{\frac{lnx}{x}}|$的图象，由此能求出函数F（x）=|${\frac{lnx}{x}}$|-f（x）在区间（0，2016）的零点个数．

解答 解：当0≤x＜2时，f（x）=$\sqrt{1-（x-1）^{2}}$，即（x-1）²+y²=1（y≥0），
当2≤x＜6时，$f（x）=\sqrt{4-{{（x-4）}^2}}$，即（x-4）²+y²=4（y≥0），
当6≤x＜14时，$f（x）=\sqrt{{4^2}-{{（x-10）}^2}}$，即（x-10）²+y²=4²（y≥0），
当14≤x＜30时，$f（x）=\sqrt{{4^3}-{{（x-27）}^2}}$，即（x-27）²+y²=4³（y≥0），
…
当2^k-2≤x＜2^k+1-2（k∈N^*）时，$f（x）=\sqrt{{4^{k-1}}-{{（{x-（{{2^{k-1}}+{2^k}-2}）}）}^2}}$，
即（x-（2^k-1+2^k-1））²+y²=4^k-1（y≥0）．
2¹⁰-2＜2016＜2¹¹-2，
∴函数f（x）在（0，2016）间的大致图象为：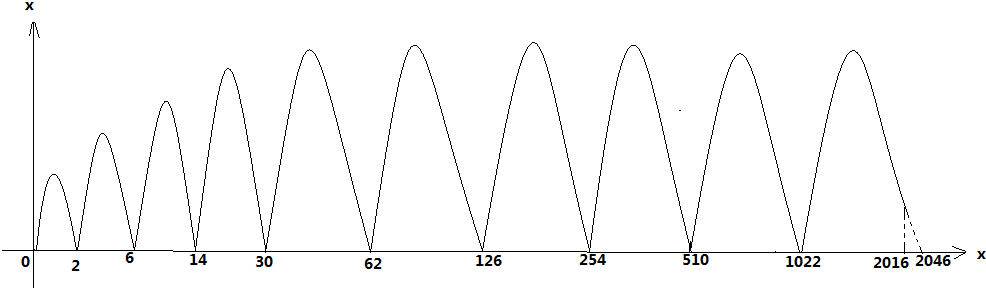


令$g（x）=\frac{lnx}{x}$，$g'（x）=\frac{1-lnx}{x^2}$，
当0＜x＜e时，g'（x）＞0，g（x）单调递增，
当x＞e时，g'（x）＜0，g（x）单调递减，
当x=e，g（x）取得最大值$g（e）=\frac{1}{e}$．
当x→0时，g（x）→-∞；当x→+∞时，g（x）＞0且g（x）→0．
故$y=|{\frac{lnx}{x}}|$的图象大致如下：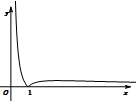

作出函数F（x）=|${\frac{lnx}{x}}$|-f（x）在区间（0，2016）的图象：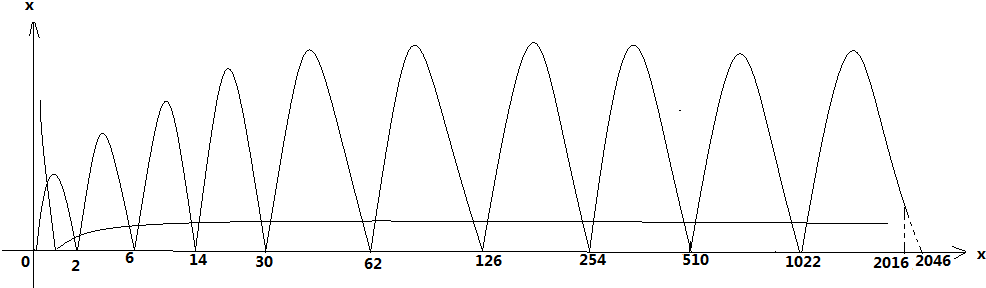

由此结合图象可知，$y=|{\frac{lnx}{x}}|$与y=f（x）在区间（0，2016）上有19个交点，
即函数F（x）=|${\frac{lnx}{x}}$|-f（x）在区间（0，2016）的零点个数为19．
故答案为：19．

点评 本题考查函数的零点个数的求法，是中档题，解题时要认真审题，注意函数性质和分类讨论思想的合理运用．