Question

4．已知函数y=f（x）为奇函数，且对定义域内的任意x都有f（1+x）=-f（1-x）．当x∈（2，3）时，f（x）=log₂（x-1）．给出以下4个结论：其中所有正确结论的为  （　　）
①函数y=f（x）的图象关于点（k，0）（k∈Z）成中心对称；
②函数y=|f（x）|是以2为周期的周期函数；
③函数y=f（|x|）在（k，k+1）（k∈Z）上单调递增；
④当x∈（-1，0）时，f（x）=-log₂（1-x）．

• A． ①②④
• B． ②③
• C． ①④
• D． ①②③④

Answer 1

分析 根据奇函数的性质和f（1+x）=-f（1-x），求出函数的周期，再由所给的解析式和周期性，求出函数在一个周期性的解析式，再画出函数在R上的图象，由图象进行逐一判断．

解答 解：令x取x+1代入f（1+x）=-f（1-x）得，f（x+2）=-f（-x）
∵函数y=f（x）为奇函数，∴f（x+2）=f（x），则函数是周期为2的周期函数，
设0＜x＜1，则2＜x+2＜3，
∵当x∈（2，3）时，f（x）=log₂（x-1），
∴f（x）=f（x+2）=log₂（x+1），
设-1＜x＜-0，则0＜-x＜1，
由f（x）=-f（-x）得，f（x）=-log₂（-x+1），
根据奇函数的性质和周期函数的性质画出函数的图象：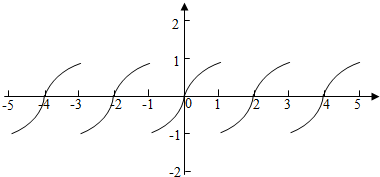

由上图得，函数y=f（x）的图象关于点（k，0）（k∈Z）成中心对称；
且函数y=|f（x）|的图象是将y=f（x）的图象在x轴下方的部分沿x轴对称过去，其他不变，
则函数y=|f（x）|是以2为周期的周期函数；
故①②④正确，
而函数y=f（|x|）=$\left\{\begin{array}{l}{f（x）\;\;x≥0}\\{f（-x）\;\;\;\;\;x＜0}\end{array}\right.$，则图象如下图：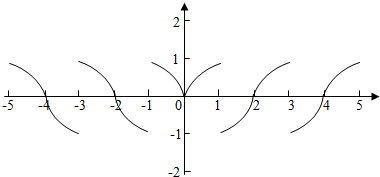

由图得，图象关于y轴对称，故y=f（|x|）在（k，k+1）（ k∈Z）上不是单调递增的，
故③不正确，
故选：A．

点评 本题考查了抽象函数的奇偶性、周期性的综合应用，以及对数函数的图象，考查了数形结合思想和转化能力，难度较大．