Question

已知函数f（x）=x³+ax²+bx-1的导函数f′（x）为偶函数，直线x-y-1=0是y=f（x）的一条切线．
（1）求a、b的值．
（2）若g（x）=-f（x）+x²+4x，求g（x）的极值．

Answer 1

解：（1）首先f′（x）=x²+2ax+b，
因为导函数f′（x）为偶函数，所以a=0，
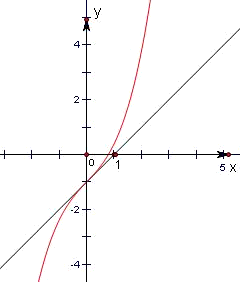
∴f（x）=x³+bx-1，此函数图象与直线x-y-1=0的一个交点是（0，1），且（0，1）是f（x）图象的一个对称中心，如图．
由于直线x-y-1=0是y=f（x）的一条切线，且直线的斜率k=1，
根据导数的几何意义知k=f′（0）=1，即b=1．
∴a=0，b=1．
（2）由（1）得：f（x）=x³+x-1，
∴g（x）=-f（x）+x²+4x=-x³+x²+3x+1
g′（x）=-x²+2x+3=-（x+1）（x-3），
当g′（x）＜0时，x＜-1或x＞3；当f′（x）＞0时，-1＜x＜3
∴函数的单调减区间是 （-∞，-1）和（3，+∞）；函数的单调增区间是（-1，3）
因此求出函数g（x）的极大值为g（3）=10，极小值为g（-1）=-．
分析：（1）先对函数进行求导，根据函数f（x）导函数f′（x）为偶函数，a值为0，再根据直线x-y-1=0是y=f（x）的一条切线，列出方程即可求出b的值；
（2）根据（1）得出的a，b的值写出g（x）的解析式，再利用导数研究它的单调性，可以得出函数g（x）的极大值与极小值．
点评：本题主要考查函数在某点取得极值的条件和导数的几何意义，以及利用导数解决函数在闭区间上的最值问题，综合性较强，属于中档题．