
设函数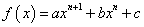
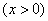 ,其中
,其中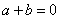 ,
,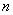 为正整数,
为正整数,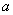 、
、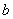 、
、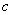 均为常数,曲线
均为常数,曲线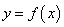 在
在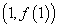 处的切线方程为
处的切线方程为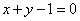 .
.
(1)求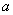 、
、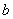 、
、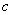 的值;
的值;
(2)求函数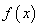 的最大值;
的最大值;
(3)证明:对任意的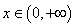 都有
都有 .(
.( 为自然对数的底)
为自然对数的底)
科目:高中数学 来源: 题型:
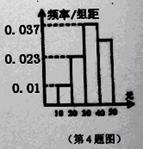
学校为了解学生课外读物方面的支出情况,抽取了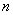 个同学进行调查,结果显示这些同学的支出都在
个同学进行调查,结果显示这些同学的支出都在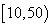 (单位:元),其中支出在
(单位:元),其中支出在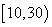 (单位:元)的同学有
(单位:元)的同学有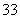 人,其频率分布直方图如下图所示,则支出在
人,其频率分布直方图如下图所示,则支出在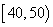 (单位:元)的同学人数是( )
(单位:元)的同学人数是( )
A.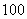 B.
B.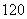 C.
C.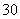 D.
D.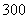
查看答案和解析>>
科目:高中数学 来源: 题型:
某单位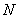 名员工参加“社区低碳你我他”活动.他们的年龄在
名员工参加“社区低碳你我他”活动.他们的年龄在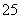 岁至
岁至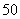 岁之间.按年龄分组:第1组
岁之间.按年龄分组:第1组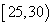 ,第
,第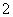 组
组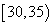 ,第3组
,第3组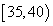 ,第
,第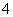 组
组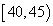 ,第
,第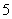 组
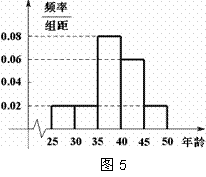
组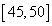 ,得到的频率分布直方图如图5所示.下表是年龄的频率分布表.
,得到的频率分布直方图如图5所示.下表是年龄的频率分布表.

| 区间 |
|
|
|
|
|
| 人数 |
|
|
|
(1)求正整数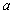 、
、 、
、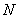 的值;
的值;
(2)现要从年龄较小的第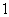 、
、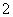 、
、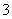 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取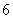 人,则年龄在第
人,则年龄在第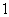 、
、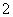 、
、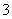 组的人数分别
组的人数分别
是多少?
(3)在(2)的条件下,从这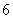 人中随机抽取
人中随机抽取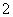 人参加社区宣传交流活动,求恰有
人参加社区宣传交流活动,求恰有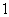 人在第
人在第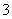 组的概率.
组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
袋中装有黑球和白球共7个,从中任取2个球都是黑球的概率为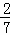 ,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取…,取球后不放回,直到两人中有一人取到白球时终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.
,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取…,取球后不放回,直到两人中有一人取到白球时终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.
(Ⅰ)求随机变量ξ的分布列及数学期望;
(Ⅱ)求乙取到白球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com