解:(1)当n=1时,2a
1-S
1=1,∴a
1=1.
又2a
n+1-S
n+1=1与2a
n-S
n=1相减得:a
n+1=2a
n,故数列{a
n}是首项为1,公比为2的等比数列,
所以
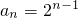
;…(4分)
(2)设a
n和a
n+1两项之间插入n个数后,这n+2个数构成的等差数列的公差为d
n,则
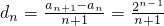
,
又(1+2+3+…+61)+61=1952,2012-1952=60,
故
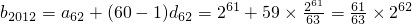
.…(9分)
(3)依题意,b
1+b
2+b
3+…+b
m=
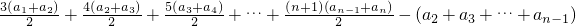
=

,
考虑到a
n+1=2a
n,令M=3a
1+5a
2+7a
3+…+(2n+1)a
n,则2M=3a
2+5a
3+7a
4+…+(2n+1)a
n+1∴2M-M=-2(a
1+a
2+a
3+…+a
n)-a
1+(2n+1)a
n+1∴M=(2n-1)2
n+1,
所以
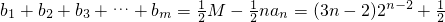
.…(14分)
分析:(1)2a
n+1-S
n+1=1与2a
n-S
n=1相减,可得数列{a
n}是首项为1,公比为2的等比数列,从而可求数列{a
n}的通项公式;
(2)设a
n和a
n+1两项之间插入n个数后,可求得
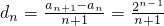
,又(1+2+3+…+61)+61=1952,2012-1952=60,从而可求b
2012的值;
(3)依题意,b
1+b
2+b
3+…+b
m=

,考虑到a
n+1=2a
n,令M=3a
1+5a
2+7a
3+…+(2n+1)a
n,则2M=3a
2+5a
3+7a
4+…+(2n+1)a
n+1,求出M=(2n-1)2
n+1,即可得到结论.
点评:本题考查数列的通项与求和,考查学生分析解决问题的能力,正确理解题意,选择正确的方法是关键.

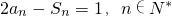 .
.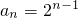 ;…(4分)
;…(4分)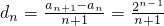 ,
,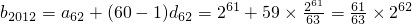 .…(9分)
.…(9分)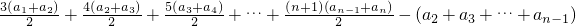 =
= ,
,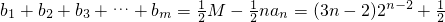 .…(14分)
.…(14分)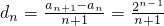 ,又(1+2+3+…+61)+61=1952,2012-1952=60,从而可求b2012的值;
,又(1+2+3+…+61)+61=1952,2012-1952=60,从而可求b2012的值; ,考虑到an+1=2an,令M=3a1+5a2+7a3+…+(2n+1)an,则2M=3a2+5a3+7a4+…+(2n+1)an+1,求出M=(2n-1)2n+1,即可得到结论.
,考虑到an+1=2an,令M=3a1+5a2+7a3+…+(2n+1)an,则2M=3a2+5a3+7a4+…+(2n+1)an+1,求出M=(2n-1)2n+1,即可得到结论.
