
分析 首先化简p,q命题,根据若p若q为真,p且q为假,得到p真q假,或p假q真,分两种情况求m的范围.
解答 解:p:函数y=x2+mx+1在(-∞-1)上单调递减,则$-\frac{m}{2}≥-1$,m≤2 …2分
q:函数y=4x2+4(m-2)x+1图象与x轴有公共点,
则△=16(m-2)2-16≥0,即(m-2)2≥1,解得m≤1或m≥3; …4分
若p或q为真,p且q为假,则p真q假,或p假q真 …6分
p真q假时,$\left\{\begin{array}{l}m≤2\\ 1<m<3\end{array}\right.$,解得1<m≤2 …8分
p假q真时,$\left\{\begin{array}{l}m>2\\ m≤1或m≥3\end{array}\right.$,解得m≥3 …10分
综上知p若q为真,p且q为假,1<m≤2或m≥3. …12分
点评 本题考查了复合命题的真假;一般的首先化简两个简单命题,然后根据复合命题的真假性得到两个命题的真假性,然后求范围.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 AF是圆O的直径,B,C是圆上两点,AB与AC的延长线分别交过点F的切线于点D,E.求证:
AF是圆O的直径,B,C是圆上两点,AB与AC的延长线分别交过点F的切线于点D,E.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
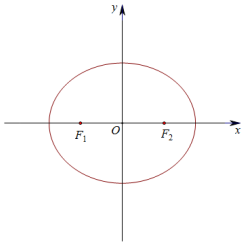 设F1,F2为椭圆$\frac{x^2}{4}$+$\frac{y^2}{3}$=1的左、右焦点,动点P的坐标为(-1,m),过点F2的直线与椭圆交于A,B两点.
设F1,F2为椭圆$\frac{x^2}{4}$+$\frac{y^2}{3}$=1的左、右焦点,动点P的坐标为(-1,m),过点F2的直线与椭圆交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+y2-4x+6y+8=0 | B. | x2+y2-4x+6y-8=0 | C. | x2+y2-4x-6y=0 | D. | x2+y2-4x+6y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com