
���� �ٸ���������ȵ����ʽ����жϣ�
�ڸ��ݴ�ǶԴ���Լ����Ҷ��������жϣ�
�۸��ݸ��Ϻ����Լ�ָ�����������ʽ�����⣬
�����ò������뷨��Ϻ����ĵ�������ֵ֮��Ĺ�ϵ�����ж���⣮
��� �⣺���ı���ABCDƽ������һ��O����$\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}$��
��$\overrightarrow{OA}$-$\overrightarrow{OB}$=$\overrightarrow{OD}$-$\overrightarrow{OC}$����$\overrightarrow{BA}$=$\overrightarrow{CD}$�����ı���ABCDΪƽ���ı��Σ���ȷ��
�ڡ�ABC�У���A��B����a��b�������Ҷ�����sinA��sinB��������֮������ʢ���ȷ��
����x2-2x��0��x��2��x��0����t=$\sqrt{{x}^{2}-2x}$����t=$\sqrt{��x-1��^{2}-1}$��0��
����$y={��\frac{1}{2}��^{\sqrt{{x^2}-2x}}}$�ʣ�0��1]����������ֵ��Ϊ��0��1]���ʢ���ȷ��
����2x+1��0��x��$-\frac{1}{2}$����$\sqrt{2x+1}=x+m$��m=$\sqrt{2x+1}$-x��
��f��x��=$\sqrt{2x+1}$-x��x��$-\frac{1}{2}$��
�����ĵ���f�䣨x��=$\frac{2}{2\sqrt{2x+1}}$-1=$\frac{1-\sqrt{2x+1}}{\sqrt{2x+1}}$��
��f�䣨x��=0��1-$\sqrt{2x+1}$=0��$\sqrt{2x+1}$=1����2x+1=1����x=0��
��x��0ʱ��f�䣨x����0��ʱ����Ϊ���������ҵ�x��+��ʱ��f��x����-�ޣ�
��$-\frac{1}{2}$��x��0ʱ��f�䣨x����0����ʱ����Ϊ��������
��x=0ʱ������ȡ�ü���ֵͬʱҲ�����ֵf��0��=1��
��f��$-\frac{1}{2}$��=0-��$-\frac{1}{2}$��=$\frac{1}{2}$��
��Ҫʹf��x��=m��������ͬ�⣬��$m��[{\frac{1}{2}��1}��$���ʢ���ȷ��
�ʴ�Ϊ���٢ڢۢ�
���� ������Ҫ�������������жϣ��漰��֪ʶ��϶࣬�ۺ��Խ�ǿ��һ�����Ѷȣ�


 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
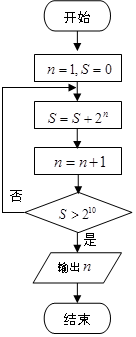
| A�� | 9 | B�� | 10 | C�� | 11 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com