
分析 (Ⅰ)根据等比数列的定义和等差中项即可求出{an}的通项公式,
(Ⅱ)根据对数的性质得到bn=log3an=n,再根据等差数列的前n项公式得到Sn,代入到${\frac{{1+2{S_n}}}{S_n}$,裂项求和即可.
解答 解:(I)设等比数列的公比为q,由题意知q>0,且3a1+2a2=a3,a1a2=a3.
∴$\left\{\begin{array}{l}{3{a}_{1}+2{a}_{1}q={a}_{1}{q}^{2}}\\{{{a}_{1}}^{2}q={a}_{1}{q}^{2}}\end{array}\right.$
解得a1=q=3,故an=3n,
(Ⅱ)bn=log3an=n,
∴Sn=$\frac{n(n+1)}{2}$,
∴${\frac{{1+2{S_n}}}{S_n}$=$\frac{2}{n(n+1)}$+2=2($\frac{1}{n}$-$\frac{1}{n+1}$)+2,
故数列{${\frac{{1+2{S_n}}}{S_n}$}的前n项和为Tn=2[(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+…+($\frac{1}{n}$-$\frac{1}{n+1}$)]+2n=2(1-$\frac{1}{n+1}$)+2n=$\frac{2{n}^{2}+4n}{n+1}$
点评 本题考查了等差数列的性质和前n项和公式和等比数列的通项公式和裂项求和,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
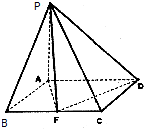 己知四棱锥P-ABCD底面ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1,F是BC的中点
己知四棱锥P-ABCD底面ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1,F是BC的中点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com