
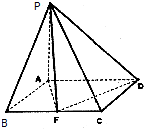
 己知四棱锥P-ABCD底面ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1,F是BC的中点
己知四棱锥P-ABCD底面ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1,F是BC的中点分析 (1)由已知可得AF=$\sqrt{2}$,DE=$\sqrt{2}$,则有DF2+AF2=AD2,则DF⊥AF.再由PA⊥平面ABCD,得DF⊥PA.由线面垂直的判定得DF⊥平面PAF,进一步得面PDF⊥面PAF.
(2)取PD的中点O,连接AO,FO,由PA=2,结合(1)可得OA=OP=OD=OF,则O为球心,解直角三角形求出三棱锥P-ADF外接球的半径,代入体积公式得答案.
解答 (1)证明:∵AD=2,AB=1,F是BC的中点,
∴AF=$\sqrt{2}$,DE=$\sqrt{2}$,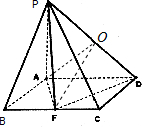
又AD=2,∴DF2+AF2=AD2,则DF⊥AF.
又PA⊥平面ABCD,∴DF⊥PA.
又PA∩AF=A,∴DF⊥平面PAF.
∵DF?面PDF,∴面PDF⊥面PAF;
(2)解:取PD的中点O,连接AO,FO,
由(1)知DF⊥PF,在Rt△PAD与Rt△PFD中,有OA=OP=OD=OF,
∴O为球心.
∵PA=2,AD=2,PD=$2\sqrt{2}$,∴球半径R=$\sqrt{2}$,
∴三棱锥P-ADF外接球的体积V=$\frac{4}{3}π{R}^{3}=\frac{8\sqrt{2}}{3}π$.
点评 本题考查平面与平面垂直的判定,考查空间想象能力和思维能力,训练了棱锥外接球体积的求法,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
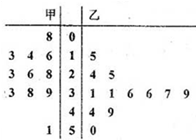 如图是甲、乙两名篮球运动员每场比赛的得分情况的茎叶图$\overline{{x}_{1}}$,$\overline{{x}_{2}}$分别表示甲乙两名运动员每场比赛得分的平均数,s1,s2分别表示甲乙两名运动员每场比赛得分的标准差,则有( )
如图是甲、乙两名篮球运动员每场比赛的得分情况的茎叶图$\overline{{x}_{1}}$,$\overline{{x}_{2}}$分别表示甲乙两名运动员每场比赛得分的平均数,s1,s2分别表示甲乙两名运动员每场比赛得分的标准差,则有( )| A. | $\overline{{x}_{1}}$<$\overline{{x}_{2}}$,s1>s2 | B. | $\overline{{x}_{1}}$<$\overline{{x}_{2}}$,s1<s2 | C. | $\overline{{x}_{1}}$>$\overline{{x}_{2}}$,s1<s2 | D. | $\overline{{x}_{1}}$>$\overline{{x}_{2}}$,s1>s2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com