
分析 (1)由甲大棚投入50万元,则乙大投棚入150万元,把a的值代入即可得出.
(2)$f(x)=80+4\sqrt{2x}+\frac{1}{4}({200-x})+120=-\frac{1}{4}x+4\sqrt{2x}+250$,依题意得$\left\{\begin{array}{l}x≥20\\ 200-x≥20\end{array}\right.⇒20≤x≤180$,通过换元利用二次函数的单调性即可得出.
解答 解:(1)∵甲大棚投入50万元,则乙大投棚入150万元,
∴$f({50})=80+4\sqrt{2×50}+\frac{1}{4}×150+120=277.5$万元.
(2)$f(x)=80+4\sqrt{2x}+\frac{1}{4}({200-x})+120=-\frac{1}{4}x+4\sqrt{2x}+250$,依题意得$\left\{\begin{array}{l}x≥20\\ 200-x≥20\end{array}\right.⇒20≤x≤180$,
故$f(x)=-\frac{1}{4}x+4\sqrt{2x}+250({20≤x≤180})$.
令$t=\sqrt{x}∈[{2\sqrt{5},6\sqrt{5}}]$,则$f(x)=-\frac{1}{4}{t^2}+4\sqrt{2}t+250=-\frac{1}{4}{({t-8\sqrt{2}})^2}+282$,
当$t=8\sqrt{2}$,即x=128时,f(x)max=282万元.
所以投入甲大棚128万元,乙大棚72万元时,总收益最大,且最大收益为282万元.
点评 本题考查了函数的应用、二次函数的单调性,考查了换元方法、推理能力与计算能力,属于中档题.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-∞,-1) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $-\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
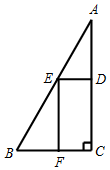 如图,在∠ABC=60°,∠C=90°,BC=40米的直角三角形地块中划出一块矩形CDEF地块进行绿化.
如图,在∠ABC=60°,∠C=90°,BC=40米的直角三角形地块中划出一块矩形CDEF地块进行绿化.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $a=\sqrt{3},b=1$ | |
| B. | 不等式f(x1)f(x2)≤4取到等号时|x1-x2|的最小值为2π | |
| C. | 函数f(x)的图象一个对称中心为 $({\frac{2}{3}π,0})$ | |
| D. | 函数f(x)在区间$[{\frac{π}{6},π}]$上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{15}{4}$ | B. | $-\frac{{\sqrt{15}}}{2}$ | C. | $\frac{15}{4}$ | D. | $\frac{{\sqrt{15}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M=N | B. | M∩N={3} | C. | M∪N={0} | D. | M∩N=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com