
【题目】一房产商竞标得一块扇形![]() 地皮,其圆心角
地皮,其圆心角![]()
![]() ,半径为
,半径为![]()
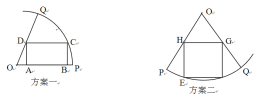
![]() ,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形
,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形![]() 的一边
的一边![]() 在半径
在半径![]() 上,
上,![]() 在圆弧上,
在圆弧上,![]() 在半径
在半径![]() ;方案二:矩形EFGH的顶点在圆弧上,顶点
;方案二:矩形EFGH的顶点在圆弧上,顶点![]() 分别在两条半径上。请你通过计算,为房产商提供决策建议。
分别在两条半径上。请你通过计算,为房产商提供决策建议。
科目:高中数学 来源: 题型:
【题目】函数f(x)=lg(x2﹣2x﹣3)的定义域为集合A,函数g(x)=2x﹣a(x≤2)的值域为集合B. (Ⅰ)求集合A,B;
(Ⅱ)已知命题p:m∈A,命题q:m∈B,若p是q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在英语中不同字母出现的频率彼此不同且相差很大,但同一个字母的使用频率相当稳定,有人统计了40多万个单词中5个元音字母的使用频率,结果如下表所示:
元音字母 | A | E | I | O | U |
频率 | 7.88% | 12.68% | 7.07% | 7.76% | 2.80% |
(1)从一本英文(小说类)书里随机选一页,统计在这一页里元音字母出现的频率;
(2)将你统计得出的频率与上表中的频率进行比较,结果是否比较接近?你认为存在差异的原因是什么.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为D的函数![]() ,若同时满足下列条件:①
,若同时满足下列条件:①![]() 在D内单调递增或单调递减;②存在区间
在D内单调递增或单调递减;②存在区间![]() ,使
,使![]() 在
在![]() 上的值域为
上的值域为![]() ,则把
,则把![]() 叫闭函数。
叫闭函数。
(1)求闭函数![]() 符合条件②的区间
符合条件②的区间![]() ;
;
(2)判断函数![]() 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)已知![]() 是正整数,且定义在
是正整数,且定义在![]() 的函数
的函数![]() 是闭函数,求正整数
是闭函数,求正整数![]() 的最小值,及此时实数k的取值范围。
的最小值,及此时实数k的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
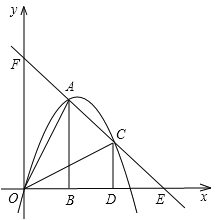
【题目】如图,把两个全等的![]() 和
和![]() 分别置于平面直角坐标系中,使直角边
分别置于平面直角坐标系中,使直角边![]() 在
在![]() 轴上,已知点
轴上,已知点![]() ,过
,过![]() 两点的直线分别交
两点的直线分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() . 抛物线
. 抛物线![]() 经过
经过![]() 三点.
三点.
(1)求该抛物线的函数解析式;
(2)点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的平行线交抛物线于点
轴的平行线交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,问是否存在这样的点
,问是否存在这样的点![]() ,使得四边形
,使得四边形![]() 为等腰梯形?若存在,求出此时点
为等腰梯形?若存在,求出此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)若![]() 沿
沿![]() 方向平移(点
方向平移(点![]() 始终在线段
始终在线段![]() 上,且不与点
上,且不与点![]() 重合),
重合),![]() 在平移的过程中与
在平移的过程中与![]() 重叠部分的面积记为
重叠部分的面积记为![]() ,试探究
,试探究![]() 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在单调递增数列![]() 中,
中,![]() ,
,![]() ,且
,且![]() 成等差数列,
成等差数列,![]() 成等比数列,
成等比数列,![]() 。
。
(Ⅰ)(ⅰ)求证:数列![]() 为等差数列;
为等差数列;
(ⅱ)求数列![]() 的通项公式。
的通项公式。
(Ⅱ)设数列![]() 的前
的前![]() 项和为
项和为![]() ,证明:
,证明:![]() ,
,![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
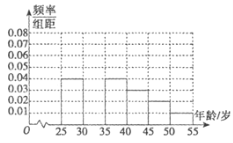
【题目】近几年骑车锻炼越来越受到人们的喜爱,男女老少踊跃参加,我校课外活动小组利用春节放假时间进行社会实践,对![]() 年龄段的人群随机抽取
年龄段的人群随机抽取![]() 人进行了一次“你是否喜欢骑车锻炼”的问卷,将被调查人员分为“喜欢骑车”和“不喜欢骑车”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次“你是否喜欢骑车锻炼”的问卷,将被调查人员分为“喜欢骑车”和“不喜欢骑车”,得到如下统计表和各年龄段人数频率分布直方图:
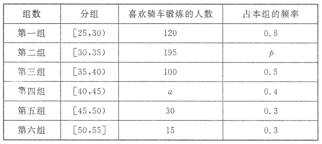
(1)补全频率分布直方图,并![]() 的值;
的值;
(2)从![]() 岁年龄段的“喜欢骑车”中采用分层抽样法抽取6人参加骑车锻炼体验活动,求其中选取2名领队来自同一组的概率。
岁年龄段的“喜欢骑车”中采用分层抽样法抽取6人参加骑车锻炼体验活动,求其中选取2名领队来自同一组的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 截以原点
截以原点![]() 为圆心的圆所得的弦长为
为圆心的圆所得的弦长为![]() 。
。
(1)求圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 切于第一象限,且与坐标轴交于点
切于第一象限,且与坐标轴交于点![]() ,当
,当![]() 长最小时,求直线
长最小时,求直线![]() 的方程;
的方程;
(3)设![]() 是圆
是圆![]() 上任意两点,点
上任意两点,点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,若直线
,若直线![]() 分别交
分别交![]() 轴于点
轴于点![]() 和
和![]() ,问
,问![]() 是否为定值?若是,请求出该定值;若不是,请说明理由。
是否为定值?若是,请求出该定值;若不是,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com