
【题目】若函数![]() 与
与![]() 在给定的区间上满足
在给定的区间上满足![]() 恒成立,则称这两个函数在该区间上“和谐”。
恒成立,则称这两个函数在该区间上“和谐”。
(1)若函数![]() 与
与![]() 在R上和谐,求实数a的取值范围;
在R上和谐,求实数a的取值范围;
(2)若函数![]() 与
与![]() 在
在![]() 上和谐,求实数a的取值范围.
上和谐,求实数a的取值范围.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)由已知条件得,需![]() 都在
都在![]() 上恒成立,或
上恒成立,或![]() 有相同的两个不等的实根,即
有相同的两个不等的实根,即 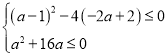 ,或
,或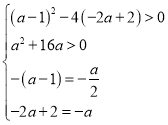 ,
,
可求得实数a的取值范围;
(2)由对数的定义域得![]() ,再由题意得
,再由题意得![]() ,由
,由![]() 和
和![]() ,可得
,可得![]() 和
和![]() ,再由
,再由![]() 讨论当
讨论当![]() 时,当
时,当![]() 时,当
时,当![]() 时,分别根据不等式的性质可得实数a的取值范围.
时,分别根据不等式的性质可得实数a的取值范围.
(1)由已知条件得,若函数![]() 与
与![]() 在R上和谐,
在R上和谐,
则需![]() 都在
都在![]() 上恒成立,或
上恒成立,或![]() 有相同的两个不等的实根,
有相同的两个不等的实根,
当![]() 都在
都在![]() 上恒成立时,则需
上恒成立时,则需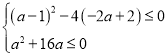 ,解得
,解得![]() ,所以
,所以![]() ;
;
当![]() 有相同的两个不等的实根时,
有相同的两个不等的实根时,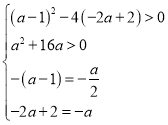 ,解得
,解得![]() ,
,
综上可得实数a的取值范围是![]() ;
;
(2)由对数的定义域可得![]() ,再由题意得
,再由题意得![]() ,
,
由![]() ,可得
,可得![]() ,所以
,所以![]() 时,
时,![]() ,
,![]() 时,
时,![]() ;
;
由![]() ,可得
,可得![]() ,所以
,所以![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
由题意要使函数![]() 与
与![]() 在
在![]() 上和谐,则
上和谐,则![]() 的两零点
的两零点![]() 之间必需无正整数,
之间必需无正整数,
又由于![]() ,所以
,所以
当![]() 时,
时,![]() ,
, ![]() ,
,![]() 之间有正整数,不满足题意;
之间有正整数,不满足题意;
当![]() 时,
时,![]() ,
, ![]() ,
,![]() 之间有正整数,不满足题意;
之间有正整数,不满足题意;
当![]() 时,
时,![]() ,满足题意.
,满足题意.
所以实数a的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】某油库的设计容量为30万吨,年初储量为10万吨,从年初起计划每月购进石油![]() 万吨,以满足区域内和区域外的需求,若区域内每月用石油1万吨,区域外前
万吨,以满足区域内和区域外的需求,若区域内每月用石油1万吨,区域外前![]() 个月的需求量
个月的需求量![]() (万吨)与
(万吨)与![]() 的函数关系为
的函数关系为![]() ,并且前4个月区域外的需求量为20万吨.
,并且前4个月区域外的需求量为20万吨.
(1)试写出第![]() 个月石油调出后,油库内储油量
个月石油调出后,油库内储油量![]() (万吨)与
(万吨)与![]() 的函数关系式;
的函数关系式;
(2)要使16个月内每月按计划购进石油之后,油库总能满足区域内和区域外的需求,且每月石油调出后,油库的石油剩余量不超出油库的容量,试确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下命题:
①若函数f(x)既是奇函数又是偶函数,则f(x)的值域为{0};
②若函数f(x)是偶函数,则f(|x|)=f(x);
③若函数f(x)在其定义域内不是单调函数,则f(x)不存在反函数;
④若函数f(x)存在反函数f﹣1(x),且f﹣1(x)与f(x)不完全相同,则f(x)与f﹣1(x)图象的公共点必在直线y=x上;
其中真命题的序号是 .(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
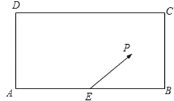
【题目】某校兴趣小组在如图所示的矩形区域![]() 内举行机器人拦截挑战赛,在
内举行机器人拦截挑战赛,在![]() 处按
处按![]() 方向释放机器人甲,同时在
方向释放机器人甲,同时在![]() 处按某方向释放机器人乙,设机器人乙在
处按某方向释放机器人乙,设机器人乙在![]() 处成功拦截机器人甲.若点
处成功拦截机器人甲.若点![]() 在矩形区域
在矩形区域![]() 内(包含边界),则挑战成功,否则挑战失败.已知
内(包含边界),则挑战成功,否则挑战失败.已知![]() 米,
米,![]() 为
为![]() 中点,机器人乙的速度是机器人甲的速度的2倍,比赛中两机器人均按匀速直线运动方式行进,记
中点,机器人乙的速度是机器人甲的速度的2倍,比赛中两机器人均按匀速直线运动方式行进,记![]() 与
与![]() 的夹角为
的夹角为![]() .
.
(1)若![]() ,
,![]() 足够长,则如何设置机器人乙的释放角度才能挑战成功?(结果精确到
足够长,则如何设置机器人乙的释放角度才能挑战成功?(结果精确到![]() );
);
(2)如何设计矩形区域![]() 的宽
的宽![]() 的长度,才能确保无论
的长度,才能确保无论![]() 的值为多少,总可以通过设置机器人乙的释放角度使机器人乙在矩形区域
的值为多少,总可以通过设置机器人乙的释放角度使机器人乙在矩形区域![]() 内成功拦截机器人甲?
内成功拦截机器人甲?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数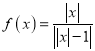 ,给出以下四个命题,其中真命题的序号是_______.
,给出以下四个命题,其中真命题的序号是_______.
①![]() 时,
时,![]() 单调递减且没有最值;
单调递减且没有最值;
②方程![]() 一定有解;
一定有解;
③如果方程![]() 有解,则解的个数一定是偶数;
有解,则解的个数一定是偶数;
④![]() 是偶函数且有最小值.
是偶函数且有最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com