
分析 (1)求出z,从而求出z的共轭复数即可;(2)①分别根据复数z是实数;是虚数;是纯虚数解方程即可,②求出$\overline{z}$,得到关于m的不等式组,解出即可.
解答 解:(1)∵(z-3)(2-i)=5,
∴z-3=$\frac{5}{2-i}$=2+i,
∴z=5+i,$\overline{z}$=5-i;
(2)z=(m2-8m+15)+(m2-5m-14)i,
①若z是实数,则m2-5m-14=0,
解得:m=7或m=-2,
若z是虚数,则m2-5m-14≠0,
解得:m≠7且m≠-2,
若z是纯虚数,则m2-8m+15=0且m2-5m-14≠0,
解得:m=3或m=5;
②∵z=(m2-8m+15)+(m2-5m-14)i,
∴$\overline{z}$=(m2-8m+15)-(m2-5m-14)i,
若$\overline{z}$对应的点在第一象限,
则$\left\{\begin{array}{l}{{m}^{2}-8m+15>0}\\{{m}^{2}-5m-14<0}\end{array}\right.$,
解得:-2<m<3或5<m<7.
点评 本题考查了复数的运算,考查复数的有关定义,是一道基础题.


科目:高中数学 来源: 题型:选择题
| A. | $y=sin(x-\frac{π}{4})$ | B. | $y=cos(x+\frac{π}{4})$ | C. | $y=sin(2x+\frac{π}{4})$ | D. | $y=cos(2x-\frac{π}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 女 | 47 36 32 48 34 44 43 47 46 41 43 42 50 43 35 49 |
| 男 | 37 35 34 43 46 36 38 40 39 32 48 33 40 34 |
| “满意”的人数 | “不满意”的人数 | 合计 | |
| 女 | 16 | ||
| 男 | 14 | ||
| 合计 | 30 |
| P(K2≥k) | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\frac{3}{2}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 3 | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
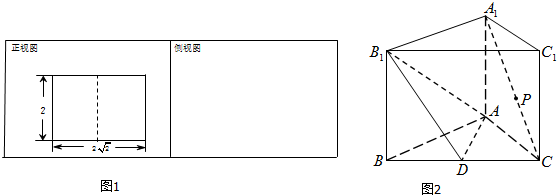
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com