
分析 (1)由已知数列递推式求得首项,得到n-1时的递推式,两式作差可得数列{an}为等比数列,由此求得数列通项公式;
(2)假设{an}中存在三项ar,as,at按某种顺序成等差数列,利用等差中项的概念得到2•2s=2r+2t,两边同除以2r得矛盾,说明假设错误.
解答 (1)解:由$\frac{1}{2}$Sn=an-1 ①,得a1=2,
且$\frac{1}{2}{S}_{n-1}={a}_{n-1}-1$ ②,
①-②得,$\frac{{a}_{n}}{{a}_{n-1}}=2$(n≥2),
∴数列{an}为等比数列,首项为2,公比为2,
∴${a}_{n}={2}^{n}$;
(2)证明:假设{an}中存在三项ar,as,at按某种顺序成等差数列,
∵${a}_{n}={2}^{n}$单增,∴ar<as<at,则2as=ar+at,即2•2s=2r+2t,
同除以2r得,2•2s-r=1+2t-r,
∵s-r≥1,t-r≥1,∴左端为偶数,右端为奇数,矛盾.
∴任意三项不可能成等差数列.
点评 本题考查数列递推式,考查了等差关系的确定,训练了反证法在存在性问题中的用法,是中档题.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:解答题
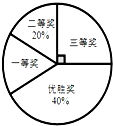 国务院办公厅在去年3月发布了《中国足球发展改革总体方案》,为进一步普及足球知识,传播足球文化,我市某县在中小学举行“足球在身边”知识竞赛活动,各类获奖学生人数比例如图的示,其中获得三等奖共50名学生,结合图中信息,解答下列问题:
国务院办公厅在去年3月发布了《中国足球发展改革总体方案》,为进一步普及足球知识,传播足球文化,我市某县在中小学举行“足球在身边”知识竞赛活动,各类获奖学生人数比例如图的示,其中获得三等奖共50名学生,结合图中信息,解答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{19}$ | B. | $\sqrt{13}$ | C. | $\sqrt{10}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com