
| A. | 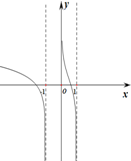 | B. | 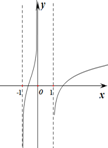 | C. | 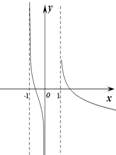 | D. | 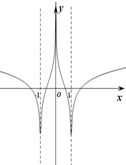 |
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:解答题
| 女 | 47 36 32 48 34 44 43 47 46 41 43 42 50 43 35 49 |
| 男 | 37 35 34 43 46 36 38 40 39 32 48 33 40 34 |
| “满意”的人数 | “不满意”的人数 | 合计 | |
| 女 | 16 | ||
| 男 | 14 | ||
| 合计 | 30 |
| P(K2≥k) | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
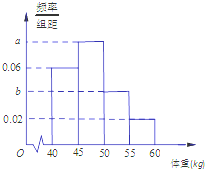 为了调查高一新生中女生的体重情况,校卫生室随机选20名女生作为样本,测量她们的体重(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中体重在区间(45,50]上的女生数与体重在区间(50,55]上的女生数之比为2:1.
为了调查高一新生中女生的体重情况,校卫生室随机选20名女生作为样本,测量她们的体重(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中体重在区间(45,50]上的女生数与体重在区间(50,55]上的女生数之比为2:1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{n+1}$ | B. | $\frac{2}{n+2}$ | C. | ($\frac{2}{3}$)n | D. | ($\frac{2}{3}$)n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
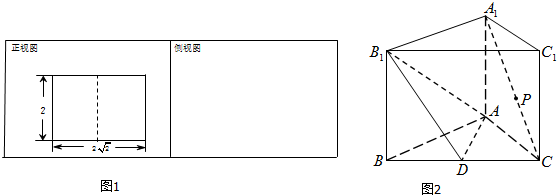
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com