
分析 根据题意,讨论x和k的取值,是否满足不等式kx2-2|x-1|+3k<0的解集为空集即可.
解答 解:当k=0时,-2|x-1|<0,解得x≠1,故不满足题意,
当x≥1时,不等式等价于kx2-2x+2+3k<0,
则k>0时,△=4-4k(2+3k)≤0,即为(3k-1)(k+1)≥0,
解得k≥$\frac{1}{3}$,
当x<1时,不等式等价于kx2+2x-2+3k<0,
则k>0时,△=4-4k(-2+3k)≤0,即为(3k+1)(k-1)≥0,
解得k≥1,
综上所述实数k的取值范围是[1,+∞).
故答案为:[1,+∞).
点评 本题考查了含有字母系数的不等式的解法与应用问题,解题时应根据题意,讨论字母系数的取值情况,从而得出正确的答案.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
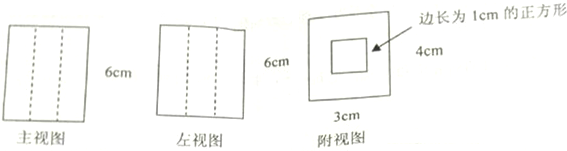
| A. | 中空的长方体,体积为72cm3 | B. | 中空的长方体,体积为66cm3 | ||
| C. | 实心长方体,体积为72cm3 | D. | 实心圆柱体,体积为66cm3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com