
分析 (1)设数列{an}的公差为d(d≥0),由已知列式求得首项和公差,则等差数列的通项公式可求;
(2)由(Ⅰ)求出等差数列的通项公式,进一步求得前n项和,取倒数后利用裂项相消法求出数列前n项和的倒数和,即可证得不等式右边,再由数列的函数特性证明左边得答案.
解答 (1)解:设数列{an}的公差为d(d≥0),由已知,
则有$\left\{{\begin{array}{l}{3{a_2}^2=75}\\{{a_1}{a_{13}}={a_4}^2}\end{array}}\right.$,∵an>0,∴$\left\{{\begin{array}{l}{{a_2}=5}\\{{a_1}{a_{13}}={a_4}^2}\end{array}}\right.$,
即$\left\{{\begin{array}{l}{{a_1}+d=5}\\{{a_1}({{a_1}+12d})={{({{a_1}+3d})}^2}}\end{array}}\right.$,解得$\left\{{\begin{array}{l}{{a_1}=5}\\{d=0}\end{array}}\right.$,或$\left\{{\begin{array}{l}{{a_1}=3}\\{d=2}\end{array}}\right.$.
an=5或an=2n+1;
(2)∵数列{an}为递增数列,∴由(Ⅰ)知an=2n+1,
∴${S}_{n}=3n+\frac{n(n-1)}{2}×2=n(n+2)$,n∈N*,
∴$\frac{1}{{S}_{n}}=\frac{1}{n(n+2)}=\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,
∴$\frac{1}{{S}_{1}}+\frac{1}{{S}_{2}}+…+\frac{1}{{S}_{n}}=\frac{1}{2}(1-\frac{1}{3})+\frac{1}{2}(\frac{1}{2}-\frac{1}{4})$$+…+\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$
=$\frac{1}{2}[(1+\frac{1}{2})-(\frac{1}{n+1}+\frac{1}{n+2})]=\frac{3}{4}-\frac{1}{2}(\frac{1}{n+1}+\frac{1}{n+2})$$<\frac{3}{4}$,
记${T}_{n}=\frac{1}{{S}_{1}}+\frac{1}{{S}_{2}}+…+\frac{1}{{S}_{n}}$
由$\frac{1}{{S}_{n}}>0$,则Tn关于n递增.
∴${T}_{n}>{T}_{1}=\frac{1}{{S}_{1}}=\frac{1}{3}$.
综上可得:$\frac{1}{3}$≤$\frac{1}{{S}_{1}}+\frac{1}{{S}_{2}}+…+\frac{1}{{S}_{n}}$$<\frac{3}{4}$.
点评 本题考查数列递推式,考查了裂项相消法求数列的前n项和,训练了利用数列的函数特性求最值,是中档题.


科目:高中数学 来源: 题型:解答题
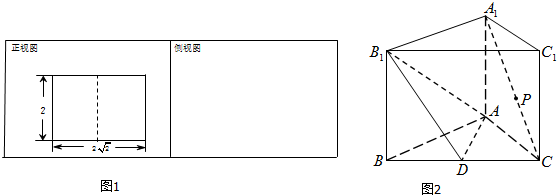
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
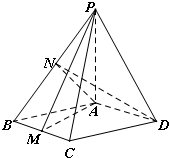 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=$\sqrt{6}$,四边形ABCD是边长为2的菱形,∠ABC=60°,M,N分别为BC和PB的中点..
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=$\sqrt{6}$,四边形ABCD是边长为2的菱形,∠ABC=60°,M,N分别为BC和PB的中点..查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
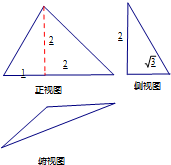
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{5\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3×106 | B. | 3×105 | C. | 0.3×106 | D. | 30×104 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com