
���� ��1������֪�����������ߵ����ʣ����Ҷ��������Ҷ����ɵ�$\frac{sinC}{2sinA-sinC}$=$\frac{sinCcosB}{sinBcosC}$������sinC��0��sinA��0��������Ǻ�����ȱ任��Ӧ�ã��������ڽǺͶ�������$cosB=\frac{1}{2}$�����B�ķ�Χ���ɵý�B��ֵ��
�����������Ǻ�����ȱ任��Ӧ�û���ɵ�T=$\frac{7}{4}$-$\frac{1}{2}$cos��2A+$\frac{��}{3}$�����ɷ�Χ$0��A��\frac{2��}{3}$������$\frac{��}{3}��2A+\frac{��}{3}��\frac{5��}{3}$���������Һ��������ʼ��ɵý�T��ȡֵ��Χ��
��� ����������Ϊ12�֣�
�⣺��1����Ϊ��$\overrightarrow m=��{sinC��{b^2}-{a^2}-{c^2}}����\overrightarrow n=��{2sinA-sinC��{c^2}-{a^2}-{b^2}}��$��$\overrightarrow m��\overrightarrow n$��
���ԣ�$\frac{sinC}{2sinA-sinC}=\frac{{{b^2}-{a^2}-{c^2}}}{{{c^2}-{a^2}-{b^2}}}=\frac{-2accosB}{-2abcosC}=\frac{{c{cosB}}}{bcosC}=\frac{sinCcosB}{sinBcosC}$������1�֣�
����sinC��0��
���ԣ�sinBcosC=2sinAcosB-sinCcosB������2�֣�
���ԣ�2sinAcosB=sinBcosC+sinCcosB=sin��B+C��=sinA������4�֣�
����sinA��0��
���ԣ�$cosB=\frac{1}{2}$��
��Ϊ��0��B���У�
���ԣ�$B=\frac{��}{3}$������6�֣�
������Ϊ��$T={sin^2}A+{sin^2}B+{sin^2}C=\frac{1}{2}��1-cos2A��+\frac{3}{4}+\frac{1}{2}��1-cos2C��$����7�֣�
=$\frac{7}{4}-\frac{1}{2}��cos2A+cos2C��=\frac{7}{4}-\frac{1}{2}[{cos2A+cos��{\frac{4��}{3}-2A}��}]$����8�֣�
=$\frac{7}{4}-\frac{1}{2}��{\frac{1}{2}cos2A-\frac{{\sqrt{3}}}{2}sin2A}��=\frac{7}{4}-\frac{1}{2}cos��{2A+\frac{��}{3}}��$����9�֣�
����$0��A��\frac{2��}{3}$��
���ԣ�$0��2A��\frac{4��}{3}$��
�ʣ�$\frac{��}{3}��2A+\frac{��}{3}��\frac{5��}{3}$������10�֣�
��ˣ�-1��cos��2A+$\frac{��}{3}$��$��\frac{1}{2}$��
���ԣ�$\frac{3}{2}$��T��$\frac{9}{4}$������12�֣�
���� ������Ҫ�������������ߵ����ʣ����Ҷ��������Ҷ��������Ǻ�����ȱ任��Ӧ�ã��������ڽǺͶ��������Һ����������ڽ��������е��ۺ�Ӧ�ã�������ת��˼�룬�����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
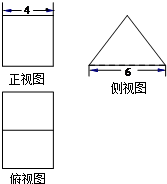 һ�������������ͼ����λ��cm����ͼ��ʾ����������ͼ�������Σ�����ͼ�ǵ��������Σ���ü�����ı����Ϊ88cm2�����Ϊ48cm3��
һ�������������ͼ����λ��cm����ͼ��ʾ����������ͼ�������Σ�����ͼ�ǵ��������Σ���ü�����ı����Ϊ88cm2�����Ϊ48cm3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8$\sqrt{3}$ | B�� | 24 | C�� | 16$\sqrt{3}$ | D�� | 24$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�2�� | B�� | ��-�ޣ�2] | C�� | ��2��+�ޣ� | D�� | [2��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
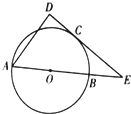 ��ͼ��ABΪԲO��ֱ����EΪAB���ӳ�����һ�㣬��E��ԲO�����ߣ��е�ΪC����A��ֱ��EC�Ĵ��ߣ�����ΪD����AB=4��CE=2$\sqrt{3}$����AD=��������
��ͼ��ABΪԲO��ֱ����EΪAB���ӳ�����һ�㣬��E��ԲO�����ߣ��е�ΪC����A��ֱ��EC�Ĵ��ߣ�����ΪD����AB=4��CE=2$\sqrt{3}$����AD=��������| A�� | 3 | B�� | 6 | C�� | 2 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
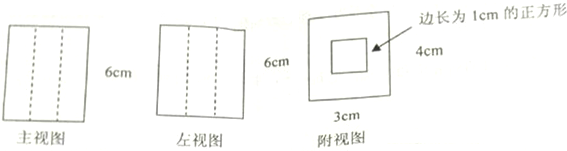
| A�� | �пյij����壬���Ϊ72cm3 | B�� | �пյij����壬���Ϊ66cm3 | ||
| C�� | ʵ�ij����壬���Ϊ72cm3 | D�� | ʵ��Բ���壬���Ϊ66cm3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com