
| A. | 8$\sqrt{3}$ | B. | 24 | C. | 16$\sqrt{3}$ | D. | 24$\sqrt{3}$ |
分析 由题意画出图形,设出正三棱锥的高为PO1=h,然后通过求解直角三角形把三棱锥的底面积用含有h的代数式表示,得到${V}_{P-ABC}=\frac{1}{3}{S}_{△ABC}•h=\frac{\sqrt{3}}{4}(6h-{h}^{2})h$,再由基本不等式求得最值.
解答 解:如图,
P-ABC是球O的内接正三棱锥,设它的高为PO1=h,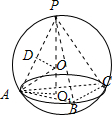
PO=AO=BO=CO=3,则O1为正三角形ABC的中心,
球心O在PO1上,
∴$A{O}_{1}=\frac{2}{3}AB•sin60°=\frac{\sqrt{3}}{3}AB$,即AB=$\sqrt{3}$AO1,
在Rt△AOO1中,$A{O}_{1}=\sqrt{A{O}^{2}-O{{O}_{1}}^{2}}=\sqrt{{3}^{2}-(h-3)^{2}}$=$\sqrt{6h-{h}^{2}}$.
∴AB=$\sqrt{3}A{O}_{1}=\sqrt{3}\sqrt{6h-{h}^{2}}$.
∴${S}_{△ABC}=\frac{1}{2}A{B}^{2}sin60°=\frac{\sqrt{3}}{4}(6h-{h}^{2})$,
${V}_{P-ABC}=\frac{1}{3}{S}_{△ABC}•h=\frac{\sqrt{3}}{4}(6h-{h}^{2})h$=$\frac{\sqrt{3}}{8}(12-2h)h•h≤\frac{\sqrt{3}}{8}×[\frac{(12-2h)+h+h}{3}]^{3}=8\sqrt{3}$.
当且仅当12-2h=h,即h=4时等号成立.
∴半径为3的球的内接正三棱锥P-ABC体积的最大值为$8\sqrt{3}$.
故选:A.
点评 本题考查棱柱、棱锥、棱台的体积,考查数学转化思想方法和数形结合的解题思想方法,是中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 50 | B. | 60 | C. | 70 | D. | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 3-$\sqrt{3}$ | C. | 9 | D. | 9-6$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com