
分析 以B为原点,以BC所在的直线为x轴,建立直角坐标系,设点P(x,0),由题意求得其它各点的坐标,计算$\overrightarrow{AP}$•$\overrightarrow{AQ}$=-x2+$\sqrt{7}$x+3,0≤x≤$\sqrt{7}$.再利用二次函数的性质求得它的最大值.
解答 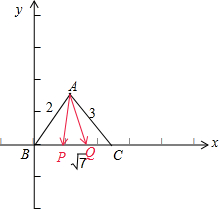 解:△ABC中,AB=2,AC=3,BC=$\sqrt{7}$,P,Q为BC边上的动点且BP=CQ,
解:△ABC中,AB=2,AC=3,BC=$\sqrt{7}$,P,Q为BC边上的动点且BP=CQ,
∴cosB=$\frac{4+7-9}{2•2•\sqrt{7}}$=$\frac{\sqrt{7}}{14}$,sinB=$\sqrt{{1-cos}^{2}B}$=$\frac{3\sqrt{21}}{14}$,以B为原点,以BC所在的直线为x轴,建立直角坐标系,
则可得B(0,0),C($\sqrt{7}$,0),A($\frac{\sqrt{7}}{7}$,$\frac{3\sqrt{21}}{7}$).
设点P(x,0),∵$\overrightarrow{BP}$=$\overrightarrow{QC}$,∴x=$\sqrt{7}$-xQ,求得xQ=$\sqrt{7}$-x,即Q($\sqrt{7}$-x,0),0≤x≤$\sqrt{7}$.
则$\overrightarrow{AP}$•$\overrightarrow{AQ}$=(x-$\frac{\sqrt{7}}{7}$,-$\frac{3\sqrt{21}}{7}$)•($\frac{6\sqrt{7}}{7}$-x,-$\frac{3\sqrt{21}}{7}$)=-x2+$\sqrt{7}$x+3,
故当x=$\frac{\sqrt{7}}{2}$时,即P、Q为线段BC的中点时,$\overrightarrow{AP}$•$\overrightarrow{AQ}$ 取得最大值为$\frac{19}{4}$,
故答案为:$\frac{19}{4}$.
点评 本题主要考查两个向量坐标形式的运算,二次函数的性质,属于中档题.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{19}$ | B. | $\sqrt{13}$ | C. | $\sqrt{10}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8$\sqrt{3}$ | B. | 24 | C. | 16$\sqrt{3}$ | D. | 24$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com