
分析 构造基本不等式的结构,利用基本不等式的性质即可得到答案.
解答 解:∵x<$\frac{1}{2}$,2x-1<0,则1-2x>0;
函数y=2x+$\frac{1}{2x-1}$
?y=2x-1+$\frac{1}{2x-1}$+1
?y=-(1-2x+$\frac{1}{1-2x}$)+1
?-(y-1)=1-2x+$\frac{1}{1-2x}$
∵1-2x>0,
∴1-2x+$\frac{1}{1-2x}$$≥2\sqrt{\frac{1}{1-2x}•(1-2x)}$=2,
(当且仅当x=$-\frac{1}{2}$时,等号成立),
所以:-(y-1)≥2⇒y≤-1
故答案为:-1.
点评 本题考查基本不等式的构造思想,整体思想,属于基本不等式的变形应用型题,使用时要注意“一正,二定,三相等”.属于中档题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 3 | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
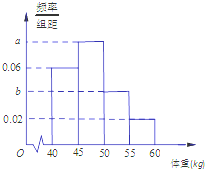 为了调查高一新生中女生的体重情况,校卫生室随机选20名女生作为样本,测量她们的体重(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中体重在区间(45,50]上的女生数与体重在区间(50,55]上的女生数之比为2:1.
为了调查高一新生中女生的体重情况,校卫生室随机选20名女生作为样本,测量她们的体重(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中体重在区间(45,50]上的女生数与体重在区间(50,55]上的女生数之比为2:1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
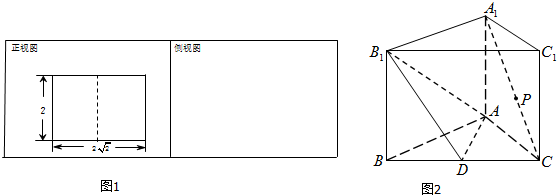
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
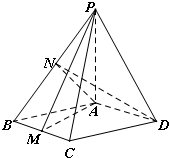 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=$\sqrt{6}$,四边形ABCD是边长为2的菱形,∠ABC=60°,M,N分别为BC和PB的中点..
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=$\sqrt{6}$,四边形ABCD是边长为2的菱形,∠ABC=60°,M,N分别为BC和PB的中点..查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com