
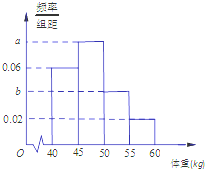
 Ϊ�˵����һ������Ů�������������У���������ѡ20��Ů����Ϊ�������������ǵ����أ���λ��kg������õ��������ݰ������䣨40��45]����45��50]����50��55]����55��60]���з��飬�õ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ����֪���������������䣨45��50]�ϵ�Ů���������������䣨50��55]�ϵ�Ů����֮��Ϊ2��1��
Ϊ�˵����һ������Ů�������������У���������ѡ20��Ů����Ϊ�������������ǵ����أ���λ��kg������õ��������ݰ������䣨40��45]����45��50]����50��55]����55��60]���з��飬�õ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ����֪���������������䣨45��50]�ϵ�Ů���������������䣨50��55]�ϵ�Ů����֮��Ϊ2��1������ ��1������Ƶ�ʵ�������С���Ƶ�ʺ�Ϊ1���������a��b�ķ����飬��֮����a��b��ֵ��
��2�����ݸ��ʵ�������ɵô𰸣��ֱ�������������¼����ӣ�50��60]�������ȡ2����������¼����������������ǵı�ֵ���ɣ�
��� �⣺��1�����������������䣨45��50]�ϵ�Ů����a��5��20=100a���ˣ���
���������������䣨50��55]�ϵ�Ů����b��5��20=100b���ˣ���
�����⣬��100a=2��100b����a=2b�٣�--------��2�֣�
����Ƶ�ʷֲ�ֱ��ͼ��֪��0.02+b+0.06+a����5�ڣ�--------��4�֣�
�����٢ڵã�a=0.08��b=0.04��--------��6�֣�
��2�����������������䣨50��55]�ϵ�Ů����0.04��5��20=4�ˣ�
���������䣨55��60]�ϵ�Ů����0.2��5��20=2�ˣ�
��֪����6��Ů���������ȡ���˹���15�������
��֪���������ڣ�55��60]�ϵ�Ů��������һ�˹���9�������
�ǡ������������������䣨50��60]�ϵ�Ů�������ȡ���ˣ�
���������䣨55��60]�ϵ�Ů��������һ�˱����С�Ϊ�¼�M��
��$P��M��=\frac{9}{15}=\frac{3}{5}$��-------��12�֣�
���� ���⿼���Ƶ���ֲ�ֱ��ͼ������������ͳ��ͼ��ȡ��Ϣ������������ͳ��ͼ��ȡ��Ϣʱ����������۲졢�������о�ͳ��ͼ������������ȷ���жϺͽ�����⣮


 �Űٷֿ�ʱ����ϵ�д�
�Űٷֿ�ʱ����ϵ�д� ������״Ԫ��ҵϵ�д�
������״Ԫ��ҵϵ�д� ��ʱ�ƿ�������ϰϵ�д�
��ʱ�ƿ�������ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{19}$ | B�� | $\sqrt{13}$ | C�� | $\sqrt{10}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������ | B�� | .���� | C�� | �ཻ | D�� | ���п��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 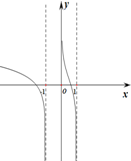 | B�� | 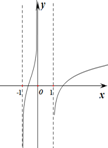 | C�� | 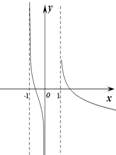 | D�� | 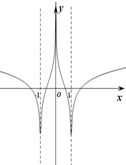 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com