
| 女 | 47 36 32 48 34 44 43 47 46 41 43 42 50 43 35 49 |
| 男 | 37 35 34 43 46 36 38 40 39 32 48 33 40 34 |
| “满意”的人数 | “不满意”的人数 | 合计 | |
| 女 | 16 | ||
| 男 | 14 | ||
| 合计 | 30 |
| P(K2≥k) | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
分析 (Ⅰ)根据所给数据,可得2×2列联表;
(Ⅱ)求出k,与临界值比较,即可得出能否在犯错误的概率不超过1%的前提下,认为该企业员工“性别”与“工作是否满意”有关.
解答 解:(Ⅰ)完成下列表格:
| “满意”的人数 | “不满意”人数 | 合计 | |
| 女 | 12 | 4 | 16 |
| 男 | 3 | 11 | 14 |
| 合计 | 15 | 15 | 30 |
点评 本题考查了列联表,独立性检验的方法等知识,考查了学生处理数据和运算求解的能力.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:选择题
| A. | [log23,2] | B. | [0,1] | C. | $[-\frac{5}{2},-1]$ | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
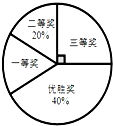 国务院办公厅在去年3月发布了《中国足球发展改革总体方案》,为进一步普及足球知识,传播足球文化,我市某县在中小学举行“足球在身边”知识竞赛活动,各类获奖学生人数比例如图的示,其中获得三等奖共50名学生,结合图中信息,解答下列问题:
国务院办公厅在去年3月发布了《中国足球发展改革总体方案》,为进一步普及足球知识,传播足球文化,我市某县在中小学举行“足球在身边”知识竞赛活动,各类获奖学生人数比例如图的示,其中获得三等奖共50名学生,结合图中信息,解答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com