
分析 分甲乙都入选、甲不入选,乙入选、甲乙都不入选,三种情况,分别求出相应的情况,即可得出结论.
解答 解:若甲乙都入选,则从其余6人中选出2人,有C62=15种,男生甲不适合担任一辩手,女生乙不适合担任四辩手,则有A44-2A33+A22=14种,故共有15×14=210种;
若甲不入选,乙入选,则从其余6人中选出3人,有C63=20种,女生乙不适合担任四辩手,则有C31A33=18种,故共有20×18=360种;
若甲乙都不入选,则从其余6人中选出4人,有C64=15种,再全排,有A44=24种,故共有15×24=360种;
综上所述,共有210+360+360=930种.
故答案为:930种.
点评 本题考查排列组合知识的运用,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\frac{3}{2}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. | 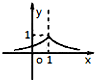 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{n+1}$ | B. | $\frac{2}{n+2}$ | C. | ($\frac{2}{3}$)n | D. | ($\frac{2}{3}$)n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 18 | C. | -15 | D. | -26 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com