
分析 (1)设出P的坐标,得到|PA|,结合双曲线方程转化为关于y的函数,利用配方法求得|PA|的最小值,并求得点P的坐标;
(2)由题意设出直线方程,联立直线方程和双曲线方程,由三角形面积列式求得直线的斜率,则答案可求.
解答 解:(1)设P(x,y),则|PA|=$\sqrt{{x}^{2}+(y-1)^{2}}=\sqrt{2+2{y}^{2}+(y-1)^{2}}=\sqrt{3(y-\frac{1}{3})^{2}+\frac{8}{3}}$.
当y=$\frac{1}{3}$时,|PA|最小,
故所求点P的坐标为($±\frac{2\sqrt{5}}{3},\frac{1}{3}$);
(2)由题知直线l的斜率存在,故可设l的方程为y=kx+1,
与双曲线方程联立得(1-2k2)x2-4kx-4=0.
则△=16(1-k2)>0且$\frac{-4}{1-2{k}^{2}}<0$,解得${k}^{2}<\frac{1}{2}$.
∴${S}_{△OMN}=\frac{1}{2}•1•|{x}_{1}-{x}_{2}|=\frac{1}{2}•\frac{\sqrt{16(1-{k}^{2})}}{1-2{k}^{2}}=2\sqrt{3}$,
解得:${k}^{2}=\frac{1}{4}$或${k}^{2}=\frac{2}{3}$(舍).
∴l的方程为y=$±\frac{1}{2}x+1$.
点评 本题考查双曲线的简单性质,考查了直线与双曲线位置关系的应用,考查计算能力,是中档题.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=2-x | B. | f(x)=x-4 | C. | f(x)=6-x | D. | f(x)=x-8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
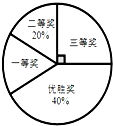 国务院办公厅在去年3月发布了《中国足球发展改革总体方案》,为进一步普及足球知识,传播足球文化,我市某县在中小学举行“足球在身边”知识竞赛活动,各类获奖学生人数比例如图的示,其中获得三等奖共50名学生,结合图中信息,解答下列问题:
国务院办公厅在去年3月发布了《中国足球发展改革总体方案》,为进一步普及足球知识,传播足球文化,我市某县在中小学举行“足球在身边”知识竞赛活动,各类获奖学生人数比例如图的示,其中获得三等奖共50名学生,结合图中信息,解答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是正方形AA1D1D和A1B1C1D1的中心.
正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是正方形AA1D1D和A1B1C1D1的中心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com