Question

20．正方体ABCD-A₁B₁C₁D₁的棱长为1，P、Q分别是正方形AA₁D₁D和A₁B₁C₁D₁的中心．
（1）证明：PQ∥平面DD₁C₁C；
（2）求线段PQ的长；
（3）求PQ与B₁C所成的角．

Answer 1

分析 （1）证明线面平行，转化成线线平行即可证明．要证明PQ∥平面DD₁C₁C；只需要在平面DD₁C₁C内找一条直线与PQ即可．
（2）求长度问题，要构造出三角形．
（3）求异面直线所成的角，分别找到两条异面直线的平行线，且交于一点，即可得到异面直线的角．

解答 解：（1）∵P、Q分别是正方形AA₁D₁D和A₁B₁C₁D₁的中心，即P、Q分别是AD₁与B₁D₁的中点；
取DD₁的中点E，取C₁D₁的中点F，连接PE、QF，EF，可得PE${\;}_{=}^{∥}$A₁D₁，QE${\;}_{=}^{∥}$C₁B₁，
∴平面QPEF是平行四边形，QP∥EF，
∵EF∈平面DD₁C₁C；
∴PQ∥平面DD₁C₁C
得证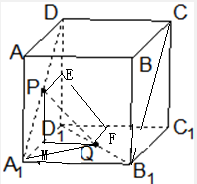

（2）取A₁D₁的中点M，连接MP，MQ，
∵P、Q分别是A₁D与B₁D₁的中点；
∴PM${\;}_{=}^{∥}$DD₁，QM${\;}_{=}^{∥}$A₁B₁，
∵DD₁⊥平面A₁B₁C₁D₁，
∴PM⊥QM
∴△MPQ是等腰直角三角形．
PM=QM=$\frac{1}{2}$
∴PQ=$\sqrt{M{Q}^{2}+M{P}^{2}}$=$\frac{\sqrt{2}}{2}$
（3）∵B₁C${\;}_{=}^{∥}$A₁D，B₁C交PQ于P，
∴PQ与B₁C所成的角即为A₁D与PQ所成的角，即是∠PA₁Q，
∵PA₁=A₁Q=$\frac{1}{2}$B₁C=$\frac{\sqrt{2}}{2}$，
由（2）可知PQ=$\frac{\sqrt{2}}{2}$，△A₁PQ是等边三角形，
∴∠PA₁Q=$\frac{π}{3}$．
所以PQ与B₁C所成的角为：$\frac{π}{3}$．

点评 本题考查线面平行证明，转化成线线平行；求长度问题，要构造出可求的三角形．
考查了异面直线所成角的求法；注重空间思维能力的培养和辅助线的经验总结．是中档题．