
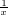 >xm对任意的x∈(0,1)恒成立,求实数m的取值范围.
>xm对任意的x∈(0,1)恒成立,求实数m的取值范围. )上递减,(-
)上递减,(- ,+∞)递增…3
,+∞)递增…3 )上递增,(-
)上递增,(- ,+∞)递减…4
,+∞)递减…4 )上递减,在(
)上递减,在( ,+∞)上递增…6
,+∞)上递增…6 时,t+2>
时,t+2> .gmin(x)=g(
.gmin(x)=g( )=
)= ln
ln =-
=- …7
…7  时,gmin(x)=g(t)=tlnt…8
时,gmin(x)=g(t)=tlnt…8 >xm>0,所以ln2
>xm>0,所以ln2 >lnxm,得m>
>lnxm,得m>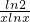 …10
…10 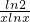 ,y′=
,y′= …11
…11 )递增,在(
)递增,在( ,+∞)递减.
,+∞)递减. )上递减,在(
)上递减,在( ,+∞)上递增,再对字母t进行分类讨论:①.当0<t≤
,+∞)上递增,再对字母t进行分类讨论:①.当0<t≤ 时,②.当t>
时,②.当t> 时,即可求出g(x)在[t,t+2](t>0)上的最小值;
时,即可求出g(x)在[t,t+2](t>0)上的最小值; >xm>0,两边取对数得ln2
>xm>0,两边取对数得ln2 >lnxm,从而有m>
>lnxm,从而有m>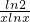 ,令y=
,令y=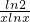 ,利用其导数研究它的单调性,即可求出实数m的取值范围.
,利用其导数研究它的单调性,即可求出实数m的取值范围.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com