
设定义在D上的函数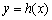 在点
在点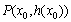 处的切线方程为
处的切线方程为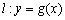 ,当
,当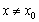 时,若
时,若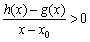 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数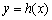 的“类对称点”,则
的“类对称点”,则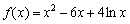 的“类对称点”的横坐标是( )
的“类对称点”的横坐标是( )
A.1 B.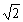 C.
C.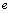 D.
D.
科目:高中数学 来源: 题型:
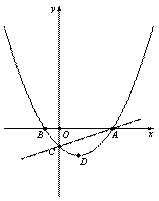
如图,已知抛物线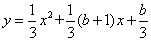 与x轴交于点A、B(点A位于点B的右侧),与y轴负半轴交于点C,顶点为D.
与x轴交于点A、B(点A位于点B的右侧),与y轴负半轴交于点C,顶点为D.
(1)点B的坐标为_____ ____,点C的坐标为__ _____;(用含b的代数式表示)
(2)当△ABD时等腰直角三角形时
①在抛物线上找一点P,使得∠PAO=∠OAC,求出符合条件的P点坐标;
②若点Q(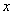 ,
,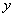 )是
)是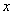 轴下方的抛物线上一点,记△QCA的面积为S,试确定使得S的值为整数的Q点的个数.
轴下方的抛物线上一点,记△QCA的面积为S,试确定使得S的值为整数的Q点的个数.
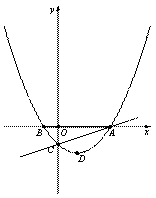
备用图
查看答案和解析>>
科目:高中数学 来源: 题型:
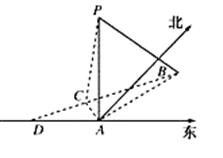
如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.
(1)求船的航行速度是每小时多少千米?
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远?
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆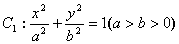 的离心率为
的离心率为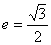 ,且过点
,且过点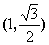 ,抛物线
,抛物线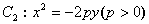 的焦点坐标为
的焦点坐标为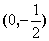 .
.
(1)求椭圆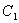 和抛物线
和抛物线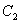 的方程;
的方程;
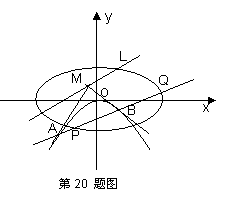
(2)若点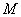 是直线
是直线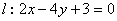 上的动点,过点
上的动点,过点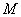 作抛物线
作抛物线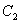 的两条切线,切点分别是
的两条切线,切点分别是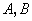 ,直线
,直线 交椭圆
交椭圆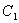 于
于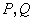 两点.
两点.
(i)求证:直线 过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;
(ii)当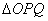 的面积取最大值时,求直线
的面积取最大值时,求直线 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com