
已知椭圆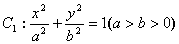 的离心率为
的离心率为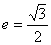 ,且过点
,且过点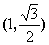 ,抛物线
,抛物线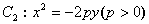 的焦点坐标为
的焦点坐标为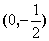 .
.
(1)求椭圆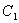 和抛物线
和抛物线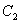 的方程;
的方程;
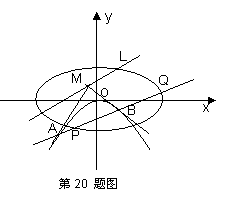
(2)若点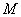 是直线
是直线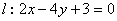 上的动点,过点
上的动点,过点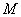 作抛物线
作抛物线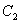 的两条切线,切点分别是
的两条切线,切点分别是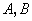 ,直线
,直线 交椭圆
交椭圆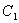 于
于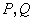 两点.
两点.
(i)求证:直线 过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;
(ii)当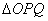 的面积取最大值时,求直线
的面积取最大值时,求直线 的方程.
的方程.
解:(1)椭圆C1: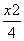 + y2=1;C2:x2=-2y ----4分
+ y2=1;C2:x2=-2y ----4分
(2)(i)设点M(x0,y0),且满足2x0-4y0+3=0,点A(x1,y1) ,B(x2 ,y2), 对于抛物线y= - 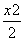 ,y¢ = - x , 则切线MA的斜率为-x1 ,从而切线MA的方程为:y–y1=-x1(x-x1),即:x1x+y+y1=0 ,同理:切线MB的方程为:x2x+y+y2=0 ,
,y¢ = - x , 则切线MA的斜率为-x1 ,从而切线MA的方程为:y–y1=-x1(x-x1),即:x1x+y+y1=0 ,同理:切线MB的方程为:x2x+y+y2=0 ,
又因为同时过M点,所以分别有:x1x0+y0+y1=0和x2x0+y0+y2=0,因此A,B同时在直线x0x+y+y0=0上,又因为:2x0-4y0+3=0,所以:AB方程可写成:y0(4x+2)+(2y-3x)= 0,显然直线AB过定点:(- 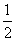 ,-
,- 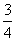 ).---------6分
).---------6分
(ii)直线AB的方程为:x0x+y+y0=0,代入椭圆方程中得:(1+4x02)x2+8x0y0x+4y02-4=0
令P(x3,y3),Q(x4,y4) , D = 16(4x02- y02+1)>0,
x3+x4 = - 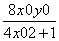 ;x3x4 =
;x3x4 = 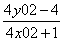
|PQ| = 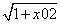 ·
·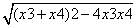 =
= 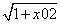 ·
·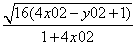 -------8分
-------8分
点O到PQ的距离为:d= 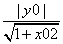
从而SDOPQ = 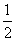 ·|PQ|·d =
·|PQ|·d = 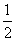 ×
×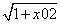 ·
·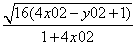 ×
×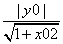
= 2×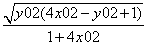 £
£ 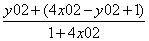 =1 ---------10分
=1 ---------10分
当且仅当y02 = 4x02- y02+1时等号成立,又2x0-4y0+3=0联立解得:x0= 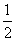 ,y0= 1或x0= -
,y0= 1或x0= - 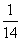 ,y0=
,y0= 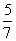 ;
;
从而所求直线AB的方程为:x+2y+2=0 或x-14y-10=0------------12分


科目:高中数学 来源: 题型:
某同学参加高校自主招生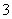 门课程的考试.假设该同学第一门课程取得优秀成绩的概率为
门课程的考试.假设该同学第一门课程取得优秀成绩的概率为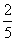 ,第二、第三门课程取得优秀成绩的概率分别为
,第二、第三门课程取得优秀成绩的概率分别为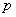 ,
,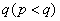 ,且不同课程是否取得优秀成绩相互独立.记
,且不同课程是否取得优秀成绩相互独立.记 为该生取得优秀成绩的课程数,其分布列为
为该生取得优秀成绩的课程数,其分布列为
|
|
|
|
|
|
|
|
|
|
|
|
(Ⅰ)求该生至少有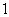 门课程取得优秀成绩的概率及求
门课程取得优秀成绩的概率及求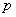 ,
,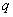 的值;
的值;
(Ⅱ)求该生取得优秀成绩课程门数的数学期望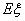 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com