练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
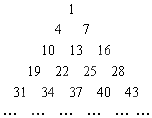
    16．将等差数列1，4，7…，按一定的规则排成了如图所示的三角形数阵．根据这个排列规则，数阵中第20行从左至右的第3个数是（　　）
    A．571B．574C．577D．580

    分析 设各行的首项组成数列{an}，则a2-a1=3，a3-a2=6，…，an-an-1=3（n-1），叠加可得：an=$\frac{3n（n-1）}{2}$+1，由此可求数阵中第20行从左至右的第3个数．

    解答 解：设各行的首项组成数列{an}，则a2-a1=3，a3-a2=6，…，an-an-1=3（n-1）
    叠加可得：an-a1=3+6+…+3（n-1）=$\frac{3n（n-1）}{2}$，
    ∴an=$\frac{3n（n-1）}{2}$+1
    ∴a20=$\frac{3×20×19}{2}$+1=571
    ∴数阵中第20行从左至右的第3个数是577．
    故选：C．

    点评 本题考查归纳推理，考查数列的特点，观察分析数字的排列规律是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

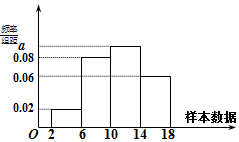    6．如图是容量为100的样本的频率分布直方图，其中a∈R．试根据图中的数据回答下列问题：
    （1）样本数据落在[2，6）内的频率为0.08；
    （2）样本数据落在[6，10）内的频数为32．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．设m，n∈N，f（x）=（1+x）m+（1+x）n．
    （1）当m=n=5时，若$f（x）={a_5}{（1-x）^5}+{a_4}{（1-x）^4}+…+{a_1}（1-x）+{a_0}$，求a0+a2+a4的值；
    （2）f（x）展开式中x的系数是9，当m，n变化时，求x2系数的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．设随机变量ξ的分布列为p（ξ=k）=$\frac{k}{3a}$（k=1，2，3，4，5），则p（ξ≤2）等于（　　）
    A．$\frac{1}{5}$B．$\frac{2}{5}$C．$\frac{1}{15}$D．$\frac{2}{15}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知圆${x^2}+{y^2}+（4-2a）x-2\sqrt{3}ay+4{a^2}-4a-12=0$，定直线l经过点A（1，0），若对任意的实数a，定直线l被圆C截得的弦长始终为定值d，求得此定值d等于（　　）
    A．$2\sqrt{7}$B．$\sqrt{31}$C．$\sqrt{34}$D．$\sqrt{37}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．若函数f（x）=ax（a＞0，且a≠1），若$f（2）=\frac{1}{4}$，则函数y=loga|x|的图象大致是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．如图所示，程序据图（算法流程图）的输出结果为（　　）
    A．$\frac{3}{4}$B．$\frac{1}{6}$C．$\frac{11}{12}$D．$\frac{25}{24}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．f（x）为奇函数，且x＞0时，f（x）=x2-2x，则x＜0时，f（x）=（　　）
    A．f（x）=x2+2-xB．f（x）=x2-2-xC．f（x）=-x2+2-xD．f（x）=-x2-2-x

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．设变量x，y满足约束条件$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y≥0}\\{x≤0}\end{array}\right.$，则z=x+2y的最小值为（　　）
    A．0B．0.5C．2D．9

    查看答案和解析>>

    同步练习册答案