
“坐标法”是以坐标系为桥梁,把几何问题转化成代数问题,通过代数运算研究图形的几何性质的方法,它是解析几何中是基本的研究方法.请用坐标法证明:
已知圆C的方程是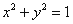 ,点
,点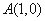 ,直线
,直线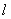 与圆C相交于P、Q两点(不同于A),
与圆C相交于P、Q两点(不同于A),
(Ⅰ)若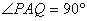 ,则直线
,则直线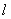 必经过圆心O;
必经过圆心O;
(Ⅱ)若直线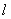 经过圆心O,则
经过圆心O,则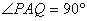 .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
矩形ABCD中,AB = 4,BC = 3,沿AC将矩形ABCD折成一个三棱锥D—ABC,当三棱锥的体积最大时,它的外接球的体积为________________
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列说法:
(1)命题“若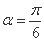 ,则
,则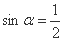 ”的否命题是假命题;
”的否命题是假命题;
(2)命题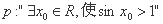 ,则
,则 ;
;
(3)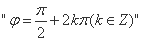 是“函数
是“函数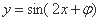 为偶函数”的充要条件;
为偶函数”的充要条件;
(4)命题 ,命题
,命题
 ,那么命题
,那么命题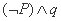 为真命题。
为真命题。
其中正确的个数是 ( )
A、4 B、3 C、2 D、1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com