练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知，则             .


         

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若均为单位向量，，，，则的最大值是

    A. 2                     B.               C.              D. 1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    椭圆方程为9+4=36，P为椭圆上任一点，F1，F2为焦点，则|PF1|+|PF2|=（   ）

       A. 2                 B. 3            C. 4                D. 6

    查看答案和解析>>

    科目：高中数学 来源： 题型：


        已知：P，Q是椭圆上两点，O为椭圆中心，OP⊥OQ，求证：

       （1）；

       （2）O到直线PQ的距离为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知不等式的解集为，则二项式展开式的常数项是

    A．5            B．-5            C．15 。            D．25

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图是某几何体的直观图与三视图的侧视图、俯视

    图. 在直观图中，2BN=AE，M是ND的中点. 侧视图是直

    角梯形，俯视图是等腰直角三角形，有关数据如图所示.

    （1）在答题纸上的虚线框内画出该几何体的正视图，

    并标上数据；

    （2）求证：EM∥平面ABC；

    （3）试问在边BC上是否存在点G，使GN⊥平面NED.

    若存在，确定点G的位置；若不存在，请说明理由

    .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知底面是边长为1的正方形，侧棱长为且侧棱与底面垂直的四棱柱的各顶点均在同一个球面上，则该球的体积为                                       （     ）

    A.         B.        C.         D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数．

    (1)求的定义域；　　　　(2)判断的单调性并证明；

    (3)方程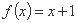是否有根？如果有根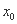，请求出一个长度为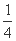的区间，使；如果没有，请说明理由？（注：区间的长度为）．

     

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    “坐标法”是以坐标系为桥梁，把几何问题转化成代数问题，通过代数运算研究图形的几何性质的方法，它是解析几何中是基本的研究方法.请用坐标法证明：

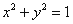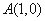    已知圆C的方程是，点，直线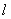与圆C相交于P、Q两点（不同于A），

    （Ⅰ）若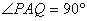，则直线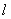必经过圆心O；

    （Ⅱ）若直线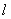经过圆心O，则.

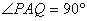    查看答案和解析>>

    同步练习册答案