
【题目】汽车厂生产![]() 三类轿车,每类轿车均有舒适型和标准型两类型号,某月的产量如下表:(单位:辆). 按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有
三类轿车,每类轿车均有舒适型和标准型两类型号,某月的产量如下表:(单位:辆). 按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有![]() 类轿车10辆.
类轿车10辆.

(1)求![]() 的值;
的值;
(2)用分层抽样的方法在![]() 类轿车中抽取一个容量为5的样本,从中任取2辆,求至少有1辆舒适型轿车的概率;
类轿车中抽取一个容量为5的样本,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从![]() 类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
试题分析:(1)设该厂本月生产轿车为n辆,由题意得,![]() ,由此先求出
,由此先求出![]() ,从而能求出
,从而能求出![]() .(2)设所抽样本中有
.(2)设所抽样本中有![]() 辆舒适型轿车,则
辆舒适型轿车,则 ![]() ,从而得到抽取了2辆舒适型轿车,3辆标准型轿车,由此利用列举法能求出从中任取2辆,至少有1辆舒适型轿车的概率.(3)利用平均数公式求出数据的平均数,通过列举得到该数与样本平均数之差的绝对值不超过0.5的数据,利用古典概型的概率公式求出概率.
,从而得到抽取了2辆舒适型轿车,3辆标准型轿车,由此利用列举法能求出从中任取2辆,至少有1辆舒适型轿车的概率.(3)利用平均数公式求出数据的平均数,通过列举得到该数与样本平均数之差的绝对值不超过0.5的数据,利用古典概型的概率公式求出概率.
试题解析:(1)设该厂这个月生产轿车![]() 辆,由已知
辆,由已知![]() ,解得
,解得![]()
则![]()
(2)设所抽取样本中有![]() 辆舒适型轿车,由题意
辆舒适型轿车,由题意![]() ,解得
,解得![]() ,
,
因此抽取的容量为5的样本中,有2辆舒适型轿车,3辆标准型轿车,
用![]() 表示2辆舒适型轿车,
表示2辆舒适型轿车,![]() 表示3辆标准型轿车,用
表示3辆标准型轿车,用![]() 表示事件“在该样本中任取2辆,其中至少有1辆舒适型轿车”.
表示事件“在该样本中任取2辆,其中至少有1辆舒适型轿车”.
则基本事件空间包含的基本事件有:![]() ,
,
![]() 共10个,事件
共10个,事件![]() 包含的基本事件有:
包含的基本事件有:![]() ,
,![]() 共7个,
共7个,
所以![]() ,即所求概率为
,即所求概率为![]() .
.
(3)样本平均数![]() ,设
,设![]() 表示事件“从样本中任取一数,该数与样本平均数之差的绝对值不超过0.5”则基本事件空间中有8个基本事件,事件
表示事件“从样本中任取一数,该数与样本平均数之差的绝对值不超过0.5”则基本事件空间中有8个基本事件,事件![]() 包含的基本事件有:9.4,8.6,9.2,8.7,9.3,9.0,共6个,所以
包含的基本事件有:9.4,8.6,9.2,8.7,9.3,9.0,共6个,所以![]() ,即所求概率为
,即所求概率为![]() .
.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:
【题目】某初级中学有三个年级,各年级男、女人数如下表:
初一年级 | 初二年级 | 初三年级 | |
女生 | 370 |
| 200 |
男生 | 380 | 370 | 300 |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求![]() 的值;
的值;
(2)用分层抽样的方法在初三年级中抽取一个容量为5的样本,求该样本中女生的人数;
(3)用随机抽样的方法从初二年级女生中选出8人,测量它们的左眼视力,结果如下:1.2,1.5,1.2,1.5,1.5,1.3,1.0,1.2.把这8人的左眼视力看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校对高一年级学生寒假参加社区服务的次数进行了统计,随机抽取了![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:
名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:

(1)求表中![]() 的值和频率分布直方图中
的值和频率分布直方图中![]() 的值,并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数;
的值,并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数;
(2)如果用分层抽样的方法从样本服务次数在![]() 和
和![]() 的人中共抽取6人,再从这6人中选2人,求2人服务次数都在
的人中共抽取6人,再从这6人中选2人,求2人服务次数都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市组织500名志愿者参加敬老活动,为方便安排任务将所有志愿者按年龄(单位:岁)分组,得到的频率分布表如下.现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人担任联系人.
年龄(岁) | 频率 | |
第1组 | [25,30) | 0.1 |
第2组 | [30,35) | 0.1 |
第3组 | [35,40) | 0.4 |
第4组 | [40,45) | 0.3 |
第5组 | [45,50) | 0.1 |
(I)应分别在第1,2,3组中抽取志愿者多少人?
(II)从这6人中随机抽取2人担任本次活动的宣传员,求至少有1人年龄在第3组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4, ![]() ,AB=2CD=8.
,AB=2CD=8.
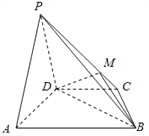
(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)当M点位于线段PC什么位置时,PA∥平面MBD?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以![]() 为顶点的五面体中,O为AB的中点,
为顶点的五面体中,O为AB的中点,
![]() 平面
平面![]() ,
, ![]() ∥
∥![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)在图中过点O作平面![]() ,使得
,使得![]() ∥平面
∥平面![]() ,并说明理由;
,并说明理由;
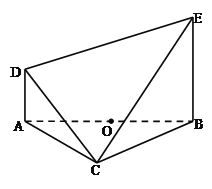
(2)求直线DE与平面CBE所成角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com