
【题目】在平面直角坐标系xOy中,已知椭圆Γ: ![]() =1,A为Γ的上顶点,P为Γ上异于上、下顶点的动点,M为x正半轴上的动点.
=1,A为Γ的上顶点,P为Γ上异于上、下顶点的动点,M为x正半轴上的动点.
(1)若P在第一象限,且|OP|= ![]() ,求P的坐标;
,求P的坐标;
(2)设P( ![]() ),若以A、P、M为顶点的三角形是直角三角形,求M的横坐标;
),若以A、P、M为顶点的三角形是直角三角形,求M的横坐标;
(3)若|MA|=|MP|,直线AQ与Γ交于另一点C,且 ![]() ,
, ![]() ,求直线AQ的方程.
,求直线AQ的方程.
【答案】
(1)解:设P(x,y)(x>0,y>0),
∵椭圆Γ: ![]() =1,A为Γ的上顶点,
=1,A为Γ的上顶点,
P为Γ上异于上、下顶点的动点,
P在第一象限,且|OP|= ![]() ,
,
∴联立 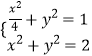 ,
,
解得P( ![]() ,
, ![]() )
)
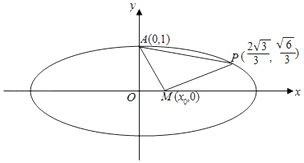
(2)解:设M(x0,0),A(0,1),
P( ![]() ),
),
若∠P=90°,则 ![]()
![]() ,即(x0﹣
,即(x0﹣ ![]() ,﹣
,﹣ ![]() )(﹣
)(﹣ ![]() ,
, ![]() )=0,
)=0,
∴(﹣ ![]() )x0+
)x0+ ![]() ﹣
﹣ ![]() =0,解得x0=
=0,解得x0= ![]() .
.
如图,若∠M=90°,则 ![]()
![]() =0,即(﹣x0,1)(
=0,即(﹣x0,1)( ![]() ﹣x0,
﹣x0, ![]() )=0,
)=0,
∴ ![]() =0,解得x0=1或x0=
=0,解得x0=1或x0= ![]() ,
,
若∠A=90°,则M点在x轴负半轴,不合题意.
∴点M的横坐标为 ![]() ,或1,或
,或1,或 ![]()
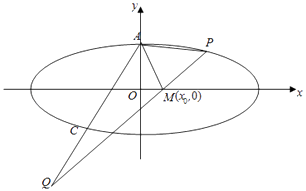
(3)解:设C(2cosα,sinα),
∵ ![]() ,A(0,1),
,A(0,1),
∴Q(4cosα,2sinα﹣1),
又设P(2cosβ,sinβ),M(x0,0),
∵|MA|=|MP|,∴x02+1=(2cosβ﹣x0)2+(sinβ)2,
整理得:x0= ![]() cosβ,
cosβ,
∵ ![]() =(4cosα﹣2cosβ,2sinα﹣sinβ﹣1),
=(4cosα﹣2cosβ,2sinα﹣sinβ﹣1), ![]() =(﹣
=(﹣ ![]() cosβ,﹣sinβ),
cosβ,﹣sinβ), ![]() ,
,
∴4cosα﹣2cosβ=﹣5cosβ,
且2sinα﹣sinβ﹣1=﹣4sinβ,
∴cosβ=﹣ ![]() cosα,且sinα=
cosα,且sinα= ![]() (1﹣2sinα),
(1﹣2sinα),
以上两式平方相加,整理得3(sinα)2+sinα﹣2=0,∴sinα= ![]() ,或sinα=﹣1(舍去),
,或sinα=﹣1(舍去),
此时,直线AC的斜率kAC=﹣ ![]() =
= ![]() (负值已舍去),如图.
(负值已舍去),如图.
∴直线AQ为y= ![]() x+1.
x+1.
【解析】(1)设P(x,y)(x>0,y>0),联立 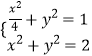 ,能求出P点坐标.(2)设M(x0,0),A(0,1),P(
,能求出P点坐标.(2)设M(x0,0),A(0,1),P( ![]() ),由∠P=90°,求出x0=
),由∠P=90°,求出x0= ![]() ;由∠M=90°,求出x0=1或x0=
;由∠M=90°,求出x0=1或x0= ![]() ;由∠A=90°,则M点在x轴负半轴,不合题意.由此能求出点M的横坐标.(3)设C(2cosα,sinα),推导出Q(4cosα,2sinα﹣1),设P(2cosβ,sinβ),M(x0,0)推导出x0=
;由∠A=90°,则M点在x轴负半轴,不合题意.由此能求出点M的横坐标.(3)设C(2cosα,sinα),推导出Q(4cosα,2sinα﹣1),设P(2cosβ,sinβ),M(x0,0)推导出x0= ![]() cosβ,从而 4cosα﹣2cosβ=﹣5cosβ,且2sinα﹣sinβ﹣1=﹣4sinβ,cosβ=﹣
cosβ,从而 4cosα﹣2cosβ=﹣5cosβ,且2sinα﹣sinβ﹣1=﹣4sinβ,cosβ=﹣ ![]() cosα,且sinα=
cosα,且sinα= ![]() (1﹣2sinα),由此能求出直线AQ.
(1﹣2sinα),由此能求出直线AQ.


科目:高中数学 来源: 题型:
【题目】某职业学校的王亮同学到一家贸易公司实习,恰逢该公司要通过海运出口一批货物,王亮同学随公司负责人到保险公司洽谈货物运输期间的投保事宜,保险公司提供了缴纳保险费的两种方案:
①一次性缴纳50万元,可享受9折优惠;
②按照航行天数交纳:第一天缴纳0.5元,从第二天起每天交纳的金额都是其前一天的2倍,共需交纳20天.
请通过计算,帮助王亮同学判断那种方案交纳的保费较低.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,x轴的非负半轴为极轴,并在两坐标系中取相同的长度单位,若直线l的极坐标方程是ρsin(θ+ ![]() )=2
)=2 ![]() ,且点P是曲线C:
,且点P是曲线C: ![]() (θ为参数)上的一个动点.
(θ为参数)上的一个动点.
(Ⅰ)将直线l的方程化为直角坐标方程;
(Ⅱ)求点P到直线l的距离的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,用35个单位正方形拼成一个矩形,点P1、P2、P3、P4以及四个标记为“▲”的点在正方形的顶点处,设集合Ω={P1 , P2 , P3 , P4},点P∈Ω,过P作直线lP , 使得不在lP上的“▲”的点分布在lP的两侧.用D1(lP)和D2(lP)分别表示lP一侧和另一侧的“▲”的点到lP的距离之和.若过P的直线lP中有且只有一条满足D1(lP)=D2(lP),则Ω中所有这样的P为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥 ![]() 中,已知
中,已知 ![]() ,
, ![]() ,
, ![]() 底面
底面 ![]() ,且
,且 ![]() ,
, ![]() ,
, ![]() 为
为 ![]() 的中点,
的中点, ![]() 在
在 ![]() 上,且
上,且 ![]() .
.
(1)求证:平面 ![]() 平面
平面 ![]() ;
;
(2)求证: ![]() 平面
平面 ![]() ;
;
(3)求三棱锥 ![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年10月18日至24日,中国共产党第十九次全国人民代表大会在北京顺利召开.大会期间,北京某高中举办了一次“喜迎十九大”的读书读报知识竞赛,参赛选手为从高一年级和高二年级随机抽取的各100名学生.图1和图2分别是高一年级和高二年级参赛选手成绩的频率分布直方图.

(1)分别计算参加这次知识竞赛的两个年级学生的平均成绩;
(2)完成下面2×2列联表,并回答能否在犯错误的概率不超过0.010的前提下,认为高一、高二两个年级学生这次读书读报知识竞赛的成绩有差异.

附:![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com