
【题目】如图,用35个单位正方形拼成一个矩形,点P1、P2、P3、P4以及四个标记为“▲”的点在正方形的顶点处,设集合Ω={P1 , P2 , P3 , P4},点P∈Ω,过P作直线lP , 使得不在lP上的“▲”的点分布在lP的两侧.用D1(lP)和D2(lP)分别表示lP一侧和另一侧的“▲”的点到lP的距离之和.若过P的直线lP中有且只有一条满足D1(lP)=D2(lP),则Ω中所有这样的P为 . 
【答案】P1、P3、P4
【解析】解:设记为“▲”的四个点为A,B,C,D,线段AB,BC,CD,DA的中点分别为E,F,G,H,
易知EFGH为平行四边形;如图所示,
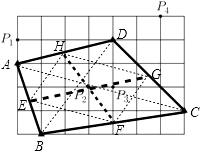
四边形ABCD两组对边中点的连线交于点P2,
即符合条件的直线lP一定经过点P2,
因此:经过点P2的直线有无数条;
同时经过点P1和P2的直线仅有1条,
同时经过点P3和P2的直线仅有1条,
同时经过点P4和P2的直线仅有1条,
所以符合条件的点为P1、P3、P4.
故答案为:P1、P3、P4.
根据任意四边形ABCD两组对边中点的连线交于一点,过此点作直线,让四边形的四个顶点不在该直线的同一侧,那么该直线两侧的四边形的顶点到直线的距离之和是相等的;由此得出结论.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知圆C: ![]() (θ为参数),点P在直线l:x+y﹣4=0上,以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系.
(θ为参数),点P在直线l:x+y﹣4=0上,以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系.
(I)求圆C和直线l的极坐标方程;
(II)射线OP交圆C于R,点Q在射线OP上,且满足|OP|2=|OR||OQ|,求Q点轨迹的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=2py(p>0)的焦点为F,A为C上异于原点的任意一点,点A到x轴的距离等于|AF|﹣1.
(1)求抛物线C的方程;
(2)直线AF与C交于另一点B,抛物线C分别在点A,B处的切线交于点P,D为y轴正半轴上一点,直线AD与C交于另一点E,且有|FA|=|FD|,N是线段AE的靠近点A的四等分点.
(i)证明点P在△NAB的外接圆上;
(ii)△NAB的外接圆周长是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+a|+|x﹣2|
(1)当a=﹣3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x﹣4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆Γ: ![]() =1,A为Γ的上顶点,P为Γ上异于上、下顶点的动点,M为x正半轴上的动点.
=1,A为Γ的上顶点,P为Γ上异于上、下顶点的动点,M为x正半轴上的动点.
(1)若P在第一象限,且|OP|= ![]() ,求P的坐标;
,求P的坐标;
(2)设P( ![]() ),若以A、P、M为顶点的三角形是直角三角形,求M的横坐标;
),若以A、P、M为顶点的三角形是直角三角形,求M的横坐标;
(3)若|MA|=|MP|,直线AQ与Γ交于另一点C,且 ![]() ,
, ![]() ,求直线AQ的方程.
,求直线AQ的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点 ![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)求曲线 ![]() 的参数方程;
的参数方程;
(2)在曲线 ![]() 上任取一点
上任取一点 ![]() ,求的
,求的 ![]() 最大值.
最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)若曲线 ![]() 在
在 ![]() 处的切线方程为
处的切线方程为 ![]() ,求
,求 ![]() 的极值;
的极值;
(2)若 ![]() ,是否存在
,是否存在 ![]() ,使
,使 ![]() 的极值大于零?若存在,求出
的极值大于零?若存在,求出 ![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
①原命题为真,它的否命题为假;
②原命题为真,它的逆命题不一定为真;
③一个命题的逆命题为真,它的否命题一定为真;
④一个命题的逆否命题为真,它的否命题一定为真.
A. ①② B. ②③
C. ③④ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com