
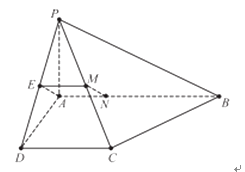
【题目】如图,在四棱锥 ![]() 中,已知
中,已知 ![]() ,
, ![]() ,
, ![]() 底面
底面 ![]() ,且
,且 ![]() ,
, ![]() ,
, ![]() 为
为 ![]() 的中点,
的中点, ![]() 在
在 ![]() 上,且
上,且 ![]() .
.
(1)求证:平面 ![]() 平面
平面 ![]() ;
;
(2)求证: ![]() 平面
平面 ![]() ;
;
(3)求三棱锥 ![]() 的体积.
的体积.
【答案】
(1)解: 证明:∵ ![]() 底面
底面 ![]() ,
, ![]() 底面
底面 ![]() ,故
,故 ![]() ;
;
又 ![]() ,
, ![]() ,因此
,因此 ![]() 平面
平面 ![]() ,又
,又 ![]() 平面
平面 ![]() ,因此平面
,因此平面 ![]() 平面
平面 ![]()
(2)解: 证明:取 ![]() 的中点
的中点 ![]() ,连接
,连接 ![]() ,
,
则 ![]() ,且
,且 ![]() ,又
,又 ![]() ,故
,故 ![]() .又
.又 ![]() ,
, ![]() ,
, ![]() ,又
,又 ![]() .
.
∴ ![]() ,
, ![]() ,且
,且 ![]() ,故四边形
,故四边形 ![]() 为平行四边形,∴
为平行四边形,∴ ![]() ,又
,又 ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,故
,故 ![]() 平面
平面 ![]() .
.
(3)解: 由 ![]() 底面
底面 ![]() ,∴
,∴ ![]() 的长就是三棱锥
的长就是三棱锥 ![]() 的高,
的高, ![]() .又
.又 ![]() ,
,
故 ![]()
【解析】(1)根据已知条件的线面垂直的性质定理可得出P A ⊥ C D ,再结合线面垂直的判定定理可得到 C D ⊥ 平面 P A D 进而得到平面P A D ⊥ 平面 PDC.(2)由题意作出辅助线根据已知可得 M E / / C D ,再结合已知条件得出ME=![]() 进而可得出 C D / / A B借助边之间的长度关系可得 M E / / A N ,且 M E = A N,得出四边形 M E A N 为平行四边形,利用边的平行关系结合线面平行的判定定理得出 M N / / 平面 P A D 。(3)由题意利用转换三棱锥的顶点把三角形BDC做为底面由已知P A = 1,借助三棱锥的体积公式
进而可得出 C D / / A B借助边之间的长度关系可得 M E / / A N ,且 M E = A N,得出四边形 M E A N 为平行四边形,利用边的平行关系结合线面平行的判定定理得出 M N / / 平面 P A D 。(3)由题意利用转换三棱锥的顶点把三角形BDC做为底面由已知P A = 1,借助三棱锥的体积公式![]() 代入数值求出结果。
代入数值求出结果。


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆Γ: ![]() =1,A为Γ的上顶点,P为Γ上异于上、下顶点的动点,M为x正半轴上的动点.
=1,A为Γ的上顶点,P为Γ上异于上、下顶点的动点,M为x正半轴上的动点.
(1)若P在第一象限,且|OP|= ![]() ,求P的坐标;
,求P的坐标;
(2)设P( ![]() ),若以A、P、M为顶点的三角形是直角三角形,求M的横坐标;
),若以A、P、M为顶点的三角形是直角三角形,求M的横坐标;
(3)若|MA|=|MP|,直线AQ与Γ交于另一点C,且 ![]() ,
, ![]() ,求直线AQ的方程.
,求直线AQ的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点 ![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)求曲线 ![]() 的参数方程;
的参数方程;
(2)在曲线 ![]() 上任取一点
上任取一点 ![]() ,求的
,求的 ![]() 最大值.
最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() .
.
(1)若函数 ![]() 的图象在点
的图象在点 ![]() 处的切线平行于直线
处的切线平行于直线 ![]() ,求
,求 ![]() 的值;
的值;
(2)讨论函数 ![]() 在定义域上的单调性;
在定义域上的单调性;
(3)若函数 ![]() 在
在 ![]() 上的最小值为
上的最小值为 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)若曲线 ![]() 在
在 ![]() 处的切线方程为
处的切线方程为 ![]() ,求
,求 ![]() 的极值;
的极值;
(2)若 ![]() ,是否存在
,是否存在 ![]() ,使
,使 ![]() 的极值大于零?若存在,求出
的极值大于零?若存在,求出 ![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若曲线f(x)= ![]() (e﹣1<x<e2﹣1)和g(x)=﹣x3+x2(x<0)上分别存在点A、B,使得△OAB是以原点O为直角顶点的直角三角形,且斜边AB的中点在y轴上,则实数a的取值范围是( )
(e﹣1<x<e2﹣1)和g(x)=﹣x3+x2(x<0)上分别存在点A、B,使得△OAB是以原点O为直角顶点的直角三角形,且斜边AB的中点在y轴上,则实数a的取值范围是( )
A.(e,e2)
B.(e, ![]() )
)
C.(1,e2)
D.[1,e)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对函数f(x),如果存在x0≠0使得f(x0)=﹣f(﹣x0),则称(x0 , f(x0))与(﹣x0 , f(﹣x0))为函数图象的一组奇对称点.若f(x)=ex﹣a(e为自然数的底数)存在奇对称点,则实数a的取值范围是( )
A.(﹣∞,1)
B.(1,+∞)
C.(e,+∞)
D.[1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com