考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由正方形性质得AB1⊥A1B,由线面垂直得A1B⊥AC1,同理,A1C⊥AC1,从而得到AC1⊥平面A1BC,由此能证明EF⊥平面A1BC.
(2)以B为原点,BA为x轴,BC为y轴,BB1为z轴,建立空间直角坐标系,利用向量法能求出二面角A-A1B-C的平角.
解答:
(1)证明:∵ABB
1A
1是正方形,∴AB
1⊥A
1B,
∵B
1C
1⊥BB
1,B
1C
1⊥A
1B
1,∴B
1C
1⊥平面ABB
1A
1,
∴B
1C
1⊥A
1B,∴A
1B⊥AC
1,

同理,A
1C⊥AC
1,
∴AC
1⊥平面A
1BC,
∵EF∥AC
1,∴EF⊥平面A
1BC.
(2)解:以B为原点,BA为x轴,BC为y轴,BB
1为z轴,
建立空间直角坐标系,
由题意知B(0,0,0),A
1(a,0,a),A(a,0,0),C(0,a,0),
=(a,0,a),
=(0,a,0),
平面BAA
1的法向量
=(0,1,0),
设平面A
1BC的法向量为
=(x,y,z),
则
,取x=1,得
=(1,0,-1),
设二面角二面角A-A
1B-C的平面角为θ,
cosθ=|cos<
,>|=|
|,
∴二面角A-A
1B-C的平角为90°.
点评:本题考查直线与平面垂直的证明,考查二面角的大小的求法,解题时要认真审题,注意向量法的合理运用.





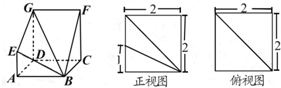 如图,多面体ABCD-EFG中,底面ABCD为正方形,GD∥FC∥AE,AE⊥平面ABCD,其正视图、俯视图及相关数据如图:
如图,多面体ABCD-EFG中,底面ABCD为正方形,GD∥FC∥AE,AE⊥平面ABCD,其正视图、俯视图及相关数据如图: