Question

已知数列{a_n}的前n项和为S_n，且满足S_n＋n＝2a_n(n∈N^*)．

(1)证明：数列{a_n＋1}为等比数列，并求数列{a_n}的通项公式；

(2)若b_n＝(2n＋1)a_n＋2n＋1，数列{b_n}的前n项和为T_n.求满足不等式>2 010的n的最小值．

 

Answer 1

【答案】

（1）a_n＝2ⁿ－1.（2）10

【解析】

试题分析：（1）由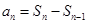将前n项和化为通项公式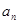关系式，利用等比数列定义证明；（2）有一个等差数列与一个等比数列对应项的积构成的新数列的和，通常将和式两边乘公比，再两式相减，得新等比数列，此法称错位相消法.

试题解析：(1)因为S_n＋n＝2a_n，所以S_n－1＝2a_n－1－(n－1)(n≥2，n∈N^*)．两式相减，得a_n＝2a_n－1＋1.

所以a_n＋1＝2(a_n－1＋1)(n≥2，n∈N^*)，所以数列{a_n＋1}为等比数列．

因为S_n＋n＝2a_n，令n＝1得a₁＝1.a₁＋1＝2，所以a_n＋1＝2ⁿ，所以a_n＝2ⁿ－1.

(2)因为b_n＝(2n＋1)a_n＋2n＋1，所以b_n＝(2n＋1)·2ⁿ.

所以T_n＝3×2＋5×2²＋7×2³＋…＋(2n－1)·2^n－1＋(2n＋1)·2ⁿ， ①

2T_n＝3×2²＋5×2³＋…＋(2n－1)·2ⁿ＋(2n＋1)·2^n＋1， ②

①－②，得－T_n＝3×2＋2(2²＋2³＋…＋2ⁿ)－(2n＋1)·2^n＋1

＝6＋2×－(2n＋1)·2^n＋1＝－2＋2^n＋2－(2n＋1)·2^n＋1＝－2－(2n－1)·2^n＋1.

所以T_n＝2＋(2n－1)·2^n＋1.

若>2 010，则>2 010，即2^n＋1>2 010.

由于2¹⁰＝1 024,2¹¹＝2 048，所以n＋1≥11，即n≥10.

所以满足不等式>2 010的n的最小值是10.

考点：等比数列的定义及判断方法；错位相消法.