
【题目】如图,在等腰梯形ABCD中,![]() ,
,![]() ,
,![]() ,E为AD中点,点O,F分别为BE,DE的中点,将
,E为AD中点,点O,F分别为BE,DE的中点,将![]() 沿BE折起到
沿BE折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面BCDE(如图).
平面BCDE(如图).
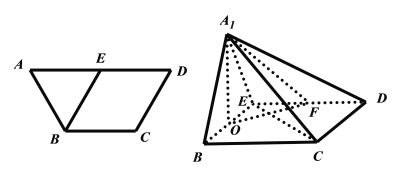
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)侧棱![]() 上是否存在点P,使得
上是否存在点P,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由
的值;若不存在,请说明理由
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)要证![]() ,只需证明
,只需证明![]() 平面BCDE即可;
平面BCDE即可;
(2)以O为原点,OB,OC,![]() 所在的直线分别为x、y、z轴建立空间直角坐标系,确定出点
所在的直线分别为x、y、z轴建立空间直角坐标系,确定出点![]() 坐标,求出平面
坐标,求出平面![]() 的法向量坐标,即可求解;
的法向量坐标,即可求解;
(3)假设满足条件的点P存在,设![]() ,
,![]() ,由四边形BCDE为菱形,且
,由四边形BCDE为菱形,且![]() ,结合(1)可知,
,结合(1)可知,![]() 平面
平面![]() ,得到
,得到![]() 为平面
为平面![]() 的一个法向量,据此可求解
的一个法向量,据此可求解![]() 的值.
的值.
(1)如图1,在等腰梯形ABCD中,由![]() ,
,![]() ,
,
![]() ,
,![]() 为
为![]() 中点,所以
中点,所以![]() 为等边三角形.
为等边三角形.
如图2,因为O为BE的中点,所以![]() ,
,
又因为平面![]() 平面BCDE,且平面
平面BCDE,且平面![]() 平面
平面![]() ,
,
所以![]() 平面BCDE,所以
平面BCDE,所以![]() .
.

(2)连结OC,由已知得![]() ,又O为BE的中点,
,又O为BE的中点,
所以![]() ,由(1)知
,由(1)知![]() 平面BCDE,
平面BCDE,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,
以O为坐标原点,OB,OC,![]() 所在的直线分别为x,y,z轴,
所在的直线分别为x,y,z轴,
建立空间直角坐标系(如图),

![]() ,
,
![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
 ,即
,即 ,令
,令![]() ,则
,则![]() ,
,
![]() 平面
平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ;
;
(3)假设侧棱![]() 上存在点P,使得
上存在点P,使得![]() 平面
平面![]() ,
,
设![]() ,
,
![]() ,
,
由四边形BCDE为菱形,![]()
![]() ,
,
![]() 分别为
分别为![]() 中点,
中点,![]() ,
,
由(1)得![]() 平面
平面![]() ,
,
![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,![]() 平面
平面![]() ,
,
![]() ,
,
所以满足条件的点![]() 存在,且
存在,且![]()


科目:高中数学 来源: 题型:
【题目】已知![]() (
(![]() 且
且![]() )是R上的奇函数,且
)是R上的奇函数,且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若关于x的方程![]() 在区间
在区间![]() 内只有一个解,求m的取值集合;
内只有一个解,求m的取值集合;
(3)设![]() ,记
,记![]() ,是否存在正整数n,使不得式
,是否存在正整数n,使不得式![]() 对一切
对一切![]() 均成立?若存在,求出所有n的值,若不存在,说明理由.
均成立?若存在,求出所有n的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的局部对称点.
的局部对称点.
(1)若![]() 且
且![]() ,证明:函数
,证明:函数![]() 必有局部对称点;
必有局部对称点;
(2)若函数![]() 在定义域
在定义域![]() 内有局部对称点,求实数
内有局部对称点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在
在![]() 上有局部对称点,求实数
上有局部对称点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”.为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图如图所示, 支持“延迟退休年龄政策”的人数与年龄的统计结果如表:

年龄(岁) |
|
|
|
|
|
支持“延迟退休年龄政策”人数 | 15 | 5 | 15 | 28 | 17 |
(I)由以上统计数据填写下面的![]() 列联表;
列联表;
年龄低于45岁的人数 | 年龄不低于45岁的人数 | 总计 | |
支持 | |||
不支持 | |||
总计 |
(II)通过计算判断是否有![]() 的把握认为以45岁为分界点的不同人群对“延迟退休年龄政策”的态度有差异.
的把握认为以45岁为分界点的不同人群对“延迟退休年龄政策”的态度有差异.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是( )
A. ![]() ,使得
,使得![]() 成立.
成立.
B. 命题![]() :任意
:任意![]() ,都有
,都有![]() ,则
,则![]() :存在
:存在![]() ,使得
,使得![]() .
.
C. 命题“若![]() 且
且![]() ,则
,则![]() 且
且![]() ”的逆命题为真命题.
”的逆命题为真命题.
D. 若数列![]() 是等比数列,
是等比数列,![]() 则
则![]() 是
是![]() 的必要不充分条件.
的必要不充分条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机卖场对市民进行国产手机认可度的调查,随机抽取![]() 名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
分组(岁) | 频数 |
|
|
|
|
|
|
|
|
|
|
合计 |
|
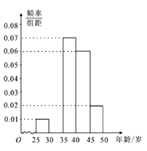
(1)求频率分布表中![]() 、
、![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)在抽取的这![]() 名市民中,按年龄进行分层抽样,抽取
名市民中,按年龄进行分层抽样,抽取![]() 人参加国产手机用户体验问卷调查,现从这
人参加国产手机用户体验问卷调查,现从这![]() 人中随机选取
人中随机选取![]() 人各赠送精美礼品一份,设这
人各赠送精美礼品一份,设这![]() 名市民中年龄在
名市民中年龄在![]() 内的人数
内的人数![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中有![]() 个白球和
个白球和![]() 个红球(
个红球(![]() ,且
,且![]() ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(1)试用含![]() 的代数式表示一次摸球中奖的概率
的代数式表示一次摸球中奖的概率![]() ;
;
(2)若![]() ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;
(3)记三次摸球恰有一次中奖的概率为![]() ,当
,当![]() 为何值时,
为何值时,![]() 取最大值.
取最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 如图,在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形,![]() 为等边三角形,平面
为等边三角形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,

(Ⅰ)设![]() 分别为
分别为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com